Consecutive Samurai Sudoku
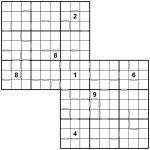
Consecutive 2-grid Samurai Sudoku
Well I promised a larger Consecutive Sudoku puzzle yesterday, and here one certainly is! It’s a 2-grid Consecutive Samurai Sudoku puzzle and the rules are essentially exactly the same as for yesterday’s puzzle except applied to a much larger grid.
The aim is to fit 1 to 9 into each of the rows, columns and 3×3 boxes of both of the two overlapping 9×9 puzzle grids, whilst obeying the consecutive constraints. In quick summary (read my full description yesterday), squares separated by a white bar contain values that are ‘consecutive’ – have a difference in value of exactly 1 – and those squares without a white bar between them are not consecutive – they have a difference in value greater than 1.
This puzzle is much trickier than my 6×6 example. It will probably take you half an hour or more to solve, of which by far the hardest part is working out how to start. Once you get going (which doesn’t require writing in ridiculous numbers of pencilmarks, I promise) it should keep flowing pretty smoothly.
If you need a hint then, the short version is this:
- You only have a few given numbers, so focus on areas around these – you don’t really need to worry about entirely empty parts of the grid far away from the givens to get going.
- Remember to solve both grids simultaneously and pay attention to the non-consecutive squares too!
- Focus on the centre 3×3 box – the information from both grids will help you make progress on it (and then from there you can actually consider both grids mostly independently)
A more detailed hint (but only a hint – not full instructions for getting going!) is this: after filling a few easy numbers around the ‘9′ in the bottom-right grid, the secret is to consider where a ‘9′ can go in the very centre box. Part of this deduction is remembering (and this is critical!) not just to pay attention to the consecutive squares but also the non-consecutive ones! Noting that the number directly below the ‘8′ in the centre 3×3 box of the top-left grid cannot possibly be a 7 or a 9 (and therefore the number to the right of that cannot be an 8, and the one to the right of that can’t be a 9) is a critical part of this process, along with a few deductions based around possible placements of 9s in the left three columns of the bottom-right 9×9 grid.
Good luck! (Once you get going this is a really fun puzzle!)
Comments are closed.

about 16 years ago
I LOVE consecutive sudoku puzzles so thanks for the challenge! This one however is still a work in progress! I couldn’t get started without the hints, but I’ve been gradually chipping away at it over the last couple of days and have finally got the bottom 9 x 9 grid filled – I’m still working on the top half but will get there in the end! It’s so much more satisfying when the level of the puzzle makes you struggle, but is achievable!
about 16 years ago
Just completed this one! Really enjoyed it thanks!
about 16 years ago
Had a couple of false starts but got there. Interesting that there are only 7 givens.
I have been also playing a standard sudoku size puzzle called Str8ts:
www . str8ts . com
It follows the consecutive idea across a crossword region (like Kakuro). It helps me with my Mah Jhong game thinking about consecutive numbers in a region.
about 16 years ago
Thanks for the comments!
Sorry the comment about Str8ts didn’t appear for a few days – it had a link in so got spam-trapped. Yes, I’ve seen Str8ts but I haven’t tried it yet. I saw the inventor was being very protective of their design by posting on a range of forums to criticise people who had created similar puzzles (not even necessarily exactly the same).
I have to be honest and say I haven’t tried one yet, but it does look quite fun. I’ve seen puzzles in Japanese puzzle magazines which are similar to this, but without being constrained to a 9×9 grid like this – I think the regions (where you can’t repeat numbers) flow across the whole width/height like in Sudoku? It might be interesting to try this type of puzzle (with ’straights’) whilst making the numbers unique only to the ‘current run’ – i.e. something along the lines of Kakuro Straights, rather than Sudoku Straights! Then I could make much larger puzzles, which would solve a bit more like Kakuro than Sudoku.
I will probably try this at some point!
about 16 years ago
Hi Spittledung – I followed your link to the str8ts puzzle and downloaded the sample book. Enjoyed these for a change.
about 16 years ago
Hello Dr. Gareth,
I have been waiting patiently since May 1 for you to give your verdict on Str8ts? I am the inventor of the puzzle and wouldn’t mind your opinion.
As for the protectionism you were referring to it was more based on the fact that certain individuals claimed the puzzle to be their invention on their websites. Taking a unique puzzle from the source is one thing but allowing their audience to believe they invented the concept is very wrong. That was my real issue.
Jeff Widderich
about 16 years ago
Hi Jeff,
When I wrote the above comment I hadn’t yet tried Str8ts, as I mentioned. When I did try them (over 2 months ago now!) I was pleasantly surprised – I already expected them to be interesting, but they had a lot more depth to them than I’d realised they would have. There were various different types of deduction to be made, and they were considerably trickier than I’d expected! (I’d imagined they would be pretty easy!)
So I think it’s a great puzzle, and I wish you the best of luck!
Gareth
about 16 years ago
Hi Gareth,
I appreciate the comments. Game and puzzle design is really about experimentation. Having a game evolve out of a search never guarantees the puzzle will be fun to play. The best looking symmetrical and well thought out ideas don’t necessarily have to have mass appeal.
Fortunately Str8ts does and as with most things sometimes ideas just come together as a package and work. When this happens. The best thing is not to ask why, but to simply enjoy the end result.
Jeff