Skyscraper Consecutive Sudoku
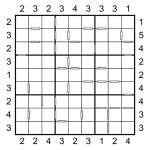
Skyscraper Consecutive Sudoku puzzle
Many of the best Sudoku variations can be combined with other variations in order to produce yet more types of puzzle. One variety I’ve personally never seen is to combine Skyscraper and Consecutive Sudoku together, so I thought I’d try it out today!
Skyscraper puzzles themselves are pleasant little puzzles where you must place 1 to 7 (or smaller) into each row and column of a grid whilst obeying ‘building height’ constraints around the edge. There’s an example 7×7 puzzle on this page over at puzzlemix. These building height constraints specify the number of notional buildings you could see whilst standing at the edge of the puzzle and looking in, whereby a taller building completely hides the view of any shorter building. The idea is that a digit ‘1′ in the grid is a building 1 storey high; a digit ‘2′ in the grid is a building 2 storeys high, and so on.
If you have a very simple 3×3 Skyscraper puzzle, here’s the potential solutions to each of the possible clues:
- 1: can be either 3 2 1 or 3 1 2, with the ‘3′ hiding both the other digits
- 2: can be 1 3 2 or 2 3 1 or 2 1 3.
- 3: can only be 1 2 3 because this is the only way to see all of the buildings.
I think that the maximum size of Skyscraper puzzle you can make without using any pre-solved numbers (givens) is 7×7, but by combining it with additional Sudoku constraints (i.e. the 3×3 boxes, and some given numbers in the puzzle already) you can make much larger puzzles.
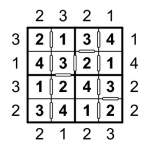
Example Consecutive Sudoku Skyscraper solution
So what we have here is a Skyscraper Sudoku – you must place 1 to 9 into each of the rows, columns and bold-lined 3×3 boxes whilst obeying the Skyscraper building height constraints around the edge of the puzzle. And then just to add an extra twist further to the puzzle, I’ve also included consecutive/non-consecutive constraints as in the previous days’ puzzles – click here for full instructions for these, but the basic idea is that a white bar separates two squares that have consecutive values (i.e. the mathematical difference is 1, so specifically 1&2, 2&3, 3&4, 4&5, 5&6, 6&7, 7&8 or 8&9) and if there’s no white bar then the difference is greater than 1 (i.e. they’re not consecutive).
I’ve attached an example 4×4 puzzle so you can be sure you understand how the Skyscraper (and consecutive) constraints work with this type of puzzle.
Good luck!
Comments are closed.

about 16 years ago
Took me two goes to get this one, made a mistake somewhere on the first attempt. Am working my way through the consecutive samurai right now