Killer CalcuDoku +/- 6×6 puzzle

There’s a lot of very interesting puzzle space to explore between the extremes of Killer Sudoku and KenKen (a trademark of Nextoy LLC, so I will always refer to this as CalcuDoku from now on, unless anyone suggests a better name!).

I’m going to define two in-between puzzles, giving a continuum like this:

  1. Killer Sudoku
  2. Killer Sudoku Pro – Killer Sudoku with extra operations (+, -, x, /)
  3. Killer CalcuDoku – Killer Sudoku Pro with repeated digits in cages, like CalcuDoku
  4. CalcuDoku – Killer CalcuDoku puzzles without box constraints (e.g. no 3×3 boxes)

To avoid confusion I’m going to draw Killer Sudoku and CalcuDoku the way they always are – with dashed-line cages in the first case and bold lines between squares for the latter (replacing the traditional Sudoku bold lines).  Then to distinguish the others, Killer Sudoku Pro will appear exactly like Killer Sudoku except that there will be additional operators within the grid (for operator-less ones I’ll include a question mark “?” or similar after each clue).  Killer CalcuDoku, meanwhile, will appear exactly like today’s puzzle – with solid cages within the main puzzle. 

Now just to spice things up further, I’m going to mess around with how the puzzles work.  Remember that the key difference between Sudoku and Killer Sudoku is that the digits now actually have value as well – so by fiddling with those values we can create an infinite range of new puzzles that solve in quite different ways.


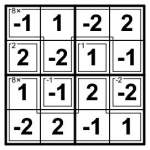
Example Killer CalcuDoku +/- solution

Today is a good example: here’s a 6×6 +/- Killer CalcuDoku.  The aim is to place -3, -2, -1, 1, 2 and 3 into each row, column and 2×3 bold-lined box, and to place numbers so that the inner cages compute to the value given when applying the stated operation to the set of numbers in that cage.  Subtraction and division are again defined as starting with the highest number in that cage (so remember that 2>-3!) and then applying all the other numbers in any order – so for example the solution to a “4-” cage could be “1 and -3″.  Confused?  See, I said it would mix things up! (1 – -3 = 4)

I’ve included an example (trivial) 4×4 Killer CalcuDoku +/- solution so you can be sure you understand how it works.  But you might not need it – it’s actually a very gentle puzzle I’ve attached, as you’ll probably soon find out… (well, once you get your head around the negative numbers!)

Good luck!