Consecutive Sudoku
Consecutive Samurai Star
Apr 17th
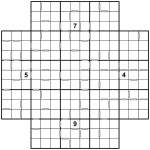
Samurai Star Consecutive puzzle
If the smaller consecutive puzzles weren’t enough of a challenge then this one should be! There are five overlaid 9×9 grids (including a ‘hidden’ one in the middle) which each need to have 1 to 9 placed into every row, column and bold-lined 3×3 box. On top of this you must obey the consecutive constraints – numbers with a white bar between are consecutive (12, 23, 34, 45, 56, 67, 78 or 89) and those without a bar between are not consecutive.
As you can see, the combination of tightly-overlaid grids and the consecutive marks means that very few givens are needed! Remember that none of these puzzles need ‘complex’ solving logic (you don’t need hidden or naked sets, X-wings or any other even more exotic strategy).
Good luck!
PS If there are any particular Sudoku or Samurai variants you’d like to see, please let me know and I’ll see what I can do!
Skyscraper Consecutive Sudoku
Apr 15th
Skyscraper Consecutive Sudoku puzzle
Many of the best Sudoku variations can be combined with other variations in order to produce yet more types of puzzle. One variety I’ve personally never seen is to combine Skyscraper and Consecutive Sudoku together, so I thought I’d try it out today!
Skyscraper puzzles themselves are pleasant little puzzles where you must place 1 to 7 (or smaller) into each row and column of a grid whilst obeying ‘building height’ constraints around the edge. There’s an example 7×7 puzzle on this page over at puzzlemix. These building height constraints specify the number of notional buildings you could see whilst standing at the edge of the puzzle and looking in, whereby a taller building completely hides the view of any shorter building. The idea is that a digit ‘1′ in the grid is a building 1 storey high; a digit ‘2′ in the grid is a building 2 storeys high, and so on.
If you have a very simple 3×3 Skyscraper puzzle, here’s the potential solutions to each of the possible clues:
- 1: can be either 3 2 1 or 3 1 2, with the ‘3′ hiding both the other digits
- 2: can be 1 3 2 or 2 3 1 or 2 1 3.
- 3: can only be 1 2 3 because this is the only way to see all of the buildings.
I think that the maximum size of Skyscraper puzzle you can make without using any pre-solved numbers (givens) is 7×7, but by combining it with additional Sudoku constraints (i.e. the 3×3 boxes, and some given numbers in the puzzle already) you can make much larger puzzles.
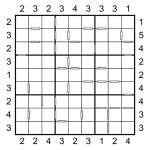
Example Consecutive Sudoku Skyscraper solution
So what we have here is a Skyscraper Sudoku – you must place 1 to 9 into each of the rows, columns and bold-lined 3×3 boxes whilst obeying the Skyscraper building height constraints around the edge of the puzzle. And then just to add an extra twist further to the puzzle, I’ve also included consecutive/non-consecutive constraints as in the previous days’ puzzles – click here for full instructions for these, but the basic idea is that a white bar separates two squares that have consecutive values (i.e. the mathematical difference is 1, so specifically 1&2, 2&3, 3&4, 4&5, 5&6, 6&7, 7&8 or 8&9) and if there’s no white bar then the difference is greater than 1 (i.e. they’re not consecutive).
I’ve attached an example 4×4 puzzle so you can be sure you understand how the Skyscraper (and consecutive) constraints work with this type of puzzle.
Good luck!
Consecutive Samurai Sudoku
Apr 14th
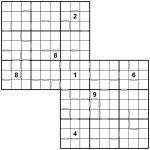
Consecutive 2-grid Samurai Sudoku
Well I promised a larger Consecutive Sudoku puzzle yesterday, and here one certainly is! It’s a 2-grid Consecutive Samurai Sudoku puzzle and the rules are essentially exactly the same as for yesterday’s puzzle except applied to a much larger grid.
The aim is to fit 1 to 9 into each of the rows, columns and 3×3 boxes of both of the two overlapping 9×9 puzzle grids, whilst obeying the consecutive constraints. In quick summary (read my full description yesterday), squares separated by a white bar contain values that are ‘consecutive’ – have a difference in value of exactly 1 – and those squares without a white bar between them are not consecutive – they have a difference in value greater than 1.
This puzzle is much trickier than my 6×6 example. It will probably take you half an hour or more to solve, of which by far the hardest part is working out how to start. Once you get going (which doesn’t require writing in ridiculous numbers of pencilmarks, I promise) it should keep flowing pretty smoothly.
If you need a hint then, the short version is this:
- You only have a few given numbers, so focus on areas around these – you don’t really need to worry about entirely empty parts of the grid far away from the givens to get going.
- Remember to solve both grids simultaneously and pay attention to the non-consecutive squares too!
- Focus on the centre 3×3 box – the information from both grids will help you make progress on it (and then from there you can actually consider both grids mostly independently)
A more detailed hint (but only a hint – not full instructions for getting going!) is this: after filling a few easy numbers around the ‘9′ in the bottom-right grid, the secret is to consider where a ‘9′ can go in the very centre box. Part of this deduction is remembering (and this is critical!) not just to pay attention to the consecutive squares but also the non-consecutive ones! Noting that the number directly below the ‘8′ in the centre 3×3 box of the top-left grid cannot possibly be a 7 or a 9 (and therefore the number to the right of that cannot be an 8, and the one to the right of that can’t be a 9) is a critical part of this process, along with a few deductions based around possible placements of 9s in the left three columns of the bottom-right 9×9 grid.
Good luck! (Once you get going this is a really fun puzzle!)
Consecutive Sudoku
Apr 13th
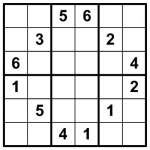
Standard Sudoku 6×6 puzzle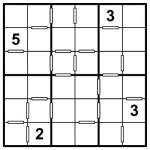
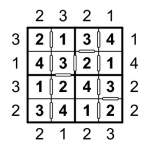
Consecutive Sudoku 6×6 puzzle
A Sudoku variant that I have always wanted to create, but somehow have just not quite ever got round to actually doing, is Consecutive Sudoku.
In Consecutive Sudoku, hollow bars between squares indicate that those two squares contain consecutive values – that is, each square is either one higher or one lower in value than the other. So if a square contains ‘3′ and there is a hollow bar between it and another square then that other square must contain either ‘2′ or ‘4′ – this is the consecutive constraint.
What makes it even more interesting is that the converse also applies – if there is not a hollow bar then the neighbouring squares are not consecutive. Therefore if a square contains ‘3′ then any neighbouring square without a hollow bar between them cannot contain either ‘2′ or ‘4′.
It might sound slightly complicated, but in fact the real beauty of this Sudoku variant is that it is actually beautifully simple when you come down to actually trying it. And what’s more, puzzles turn out to be considerably easier than you might imagine – the consecutive constraint is simple enough to trace and follow that it really helps you solve the puzzle, rather than being a complex relationship that just adds to the solving difficulty!
You also get the chance to use some new logic – it’s a very little bit like Futoshiki or Inequality Sudoku, but with (to me) a cleaner, more elegant solving path.
I’ve made an example puzzle. It’s 6×6 because it makes it easier to follow the rules if you’re new to the type – I’ll post some much larger versions soon, I promise!
Attached to this post are two puzzles, each leading to the same solution. The first is a (rather attractive circular) regular 6×6 Sudoku, which will give you the solution pretty easily if you need some help. The other is the consecutive version of the puzzle. As you can see, it has far less givens – just 4! But this is all that is needed. It shouldn’t take more than a few minutes to solve, I promise.
Standard Sudoku rules apply – place 1 to 6 into each row, column and 2×3 bold-lined box.
Good luck!
PS Just in case it isn’t obvious, when you click on the puzzle graphics they will open and load into a PDF viewer such as Adobe Acrobat (if you don’t have it click here to get it).
PPS And if you want to comment – e.g. say if you like this sort of puzzle and want to see more, or comment on how long it took you to solve it/how easy it was, then click on ‘No comments’ at the top of this post, or just click on the post title itself to open it in a new window with comments and comment box included.

Recent Comments