Samurai Variants
Wrap-around Consecutive Samurai Star
Jul 6th
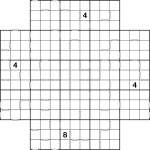
Wrap-around Consecutive Samurai Star puzzle
I seem to be posting more infrequently than I intend, so I thought I’d compensate with a puzzle that would take somewhat longer to complete! Here, then, is a wrap-around consecutive samurai star. All squares with consecutive values (a difference of 1) are marked with white bars, including those at opposite ends of rows and columns – wherever there isn’t a bar, the values are not consecutive.
The Sudoku logic takes a few twists here and there – in fact at one point near the end you will need to spot a particularly nasty hidden set in one region.
To solve the puzzle place 1 to 9 into each row, column and 3×3 box of each of the underlying 5 Sudoku grids (including the one in the centre). You’re only given 4 givens to get going, but with the consecutive information that’s all you need to find a unique solution.
Good luck! ![]()
SSSS: Skyscraper Shuriken Samurai Sudoku
Jun 5th
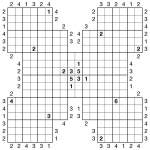
Skyscraper Shuriken Samurai Sudoku puzzle
I’m glad yesterday’s Shuriken Samurai went down well, so today I’ve upgraded it to a Skyscraper puzzle (following Christine’s request for more Skyscrapers!). This is, I think it’s fair to say, quite a bit harder than the basic Samurai yesterday was – but then any puzzle with a title this hard to say quickly really shouldn’t be able to be solved quickly either… ![]()
The rules are the same as yesterday (place 1-6 into each row, column and 2×3 box of the 13 underlying 6×6 Sudoku grids) but with the addition of Skyscraper constraints: place numbers so that the given number of digits can be ’seen’ from each external Skyscraper clue outside the grid. From the vantage point of each Skyscraper clue look along the adjacent row/column – with higher numbers obscuring all lower numbers (or those of the same value), the clue tells you how many numbers are visible. Check back to older puzzles I’ve posted for more detailed help.
Good luck! ![]()
Wrap-around Consecutive 3-grid 6×6 Samurai Skyscraper
May 18th
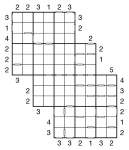
Wrap-around Consecutive 3-grid 6×6 Samurai Skyscraper puzzle
Another mouthful of a puzzle name, but in essence simply a development of the previous puzzle I posted. This time we still have the wrap-around consecutive-ness, but I’ve extended it to a samurai puzzle and added in skyscraper clues. To keep it reasonable, I’ve reduced the underylying Sudoku size to 6×6, however!
What’s particularly fun about the wrap-around markers is that they warp from one side of the puzzle to the same row/column on the opposite side – for the centre two columns this means that they constrain the values of two numbers 10 squares apart.
So the full rules are:
- Place 1 to 6 into each row, column and 2×3 bold-lined box of each of the three underlying 6×6 grids
- White bars show that adjacent cells are consecutive – i.e. 1&2, 2&3, 3&4, 4&5 or 5&6; those squares without a white bar between are non-consecutive
- White bars are shown where appropriate even on the edges of the grid – they indicate how the cell relates to the square at the far end of this row/column of numbers. Remember that the lack of such a white bar means that these wrap-around squares are non-consecutive.
- Skyscraper clues reveal how many numbers can be ’seen’ from that clue number counting in along the adjacent row/column, where higher numbers obscure all lower numbers (see previous puzzles for more detailed instructions)
Just to clarify, if adjacent numbers are equal (which is possible if they’re at far sides of the grid from one another) then these count as non-consecutive.
Good luck! ![]()
Samurai Toroidal Killer Sudoku Pro 13-grid
May 7th

Samurai Toroidal 13-grid Killer Sudoku Pro puzzle
Now this is a puzzle I can state with confidence that you won’t have seen before. It’s a Killer Sudoku Pro puzzle – i.e. a Killer Sudoku with -, x and / regions too; but more than that it’s a Samurai Killer Sudoku Pro made out of 13 grids; and then further still the cages are toroidal, both around the edge of the grid and across the gaps. In other words, the Killer Sudoku Pro regions aren’t bounded by the actual physical layout of the 13-grids – they either jump the gap (in a straight line) or wrap around the edges of the puzzle (again in a straight line, albeit one that jumps to the other side!).
If you like huge puzzles then you should really enjoy this, assuming you can print it out large enough to actually have a chance of solving it! For everyone else, I’ll post some more smaller puzzles soon! It’s not actually very difficult, logically, but completing the whole thing would still take a fair while – perhaps a couple of hours, I think.
The rules are:
- Place 1-9 into each row, column and 3×3 bold-lined box of each of the 13 underlying 9×9 Sudoku grids
- Place numbers into each dashed-line cage so that all together they give the total at the top-left of the cage once the given operation is applied – for subtraction and division start with the largest number in the cage and then subtract/divide-by the other numbers.
- Numbers can not be repeated in a cage.
- Some cages continue across the gaps – just use an imaginary straight-line rule to follow them on and find the rest of the cage (so for example if a cage runs across a gap in the 3rd row down, it continues on the other side of the gap also on the 3rd row down)
- Some cages continue across the edges of the grid – these wrap around to the same row or column on the opposite side of the puzzle
If you try it: Good Luck!
Consecutive Samurai CalcuDoku
May 5th

Consecutive Samurai CalcuDoku puzzle
Now this is an interesting puzzle! At first glance it looks like it can’t possibly have a unique solution, since there are no givens and only 9 cages on the entire 3-grid Samurai puzzle (made up of 6×6 grids). But in fact it uses only simple logic to solve, and it unravels pretty quickly once you get going. It’s a pretty powerful demonstration of how much you can strip a puzzle back and still keep it entirely reasonable in terms of difficulty. In fact it’s arguably too easy…
The rules are what you’d expect if you’ve been following previous puzzles, but in summary you must: (deep breath!)
- Place 1 to 6 into each row and column of the three underlying 6×6 grids
- Place numbers into each of the bold-lined cages so that they add up to the number at the top-left (or in the case of the 40x cage, multiply up to that value)
- Wherever a white bar divides two squares, the numbers in those two squares must be consecutive (so they must be one of these pairs: 1&2, 2&3, 3&4, 4&5 or 5&6)
- Where no white bar divides two squares, the numbers are non-consecutive
Good luck!
Samurai 5-grid Killer CalcuDoku puzzle
May 4th

Samurai 5-grid Killer Calcudoku puzzle
Here’s an interesting puzzle. It’s a 5-grid Samurai Killer CalcuDoku, which means that it has the 3×3 boxes from Killer Sudoku but otherwise works like a CalcuDoku puzzle, albeit a 5-grid Samurai one! All of the operations in this puzzle are addition, so aren’t shown.
Can you place 1 to 9 into each row, column and 3×3 box of each of the underlying 9×9 Sudoku grids, whilst also placing numbers so that each inner cage adds up to the total given at its top-left corner? Numbers can be repeated within these cages (pretty obviously, given how large some of them are!).
There are quite a lot of single digit cells, suggesting (truthfully) that this isn’t actually a very difficult puzzle – but it’s a good proof of concept, I think. You can create really huge cages if you want, without making the puzzle difficult (of course, the easiest way to solve these is to essentially ignore the cage completely, or at least until it is nearly finished). This particular puzzle does not require you to do any complex maths at all.
Good luck!
Samurai Star Killer Sudoku
Apr 29th
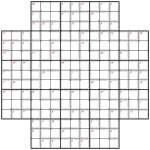
Samurai Star Killer (gentle) puzzle
“Star Killer” sounds like something out of science fiction, but it’s now definitely reality with this 5-grid Killer Sudoku puzzle. The actual Killer part uses the most basic logic imaginable, and there are a lot of ’singleton’ regions which I’ve never used in a Killer puzzle before. The reason for this is that I wanted to start at a gentle level – as a result this mostly solves like a regular Samurai Star (a.k.a. Flower Samurai) puzzle, with the Killer regions used occasionally to either get you going or help you out with a quick number along the way. It shouldn’t take you much over 20 or 30 minutes if you’ve solved this shape of Samurai before, and know what a Killer Sudoku is!
The rules are pretty simple: place 1 to 9 into each row, column and bold-lined 3×3 shape of each of the 5 underlying 9×9 grids (there’s one in the centre too), whilst also placing numbers so that the total in each dashed-line cage is equal to that given in the top-left corner. You may not repeat a number within a dashed-line cage.
The puzzle has rotation symmetry order 4, so the cages are in a pleasing pattern I hope – I particularly like the hole in the square in the centre! I think by and large that if you can create the cages or givens in a puzzle with the same order of symmetry that you have for the grid layout itself that this generally leads to a more pleasing appearance for the puzzle; but more than this, I find that this tends to follow through with the solving process, and you end up with pieces of the puzzle that feel ’sympathetic’ to one another, since the symmetry leads to related discoveries. However it’s perhaps not clear that this solving benefit carries through to a puzzle this large, and it’s probably the case that a puzzle with entirely random cages would feel just the same to actually solve at this size. But it wouldn’t look as nice!
Coming up in the following days I’m going to experiment in the space between Killer Sudoku and Ken Ken™ – in other words, using more operations than just addition, and possibly allowing repeated numbers in cages (although not on puzzles with 1-9 to place!). I already came across a puzzle called ‘Killer Sudoku Pro’ in the Saturday Telegraph newspaper (UK) – in this they keep the Killer Sudoku rules about not repeating digits in a cage, but specify different operations for cages (in actual fact the rules aren’t stated next to the puzzle in full, but I presume repeated digits are disallowed - it certainly solves okay with that assumption!). I haven’t seen anything precisely like that elsewhere and I thought it was actually quite fun (it wasn’t too hard!) so I’ll definitely try making some of those soon for sure. If you have any other ideas for how to mix these different types together feel free to post a comment!
Good luck!
Consecutive 5-grid Samurai Sudoku
Apr 24th
I thought it would be a nice idea to create a large Consecutive Sudoku for the weekend! And so here one is: a 5-grid Samurai Consecutive Sudoku. As you can see, there are very few givens to start with, so it will hopefully be at least a bit of a challenge! (It shouldn’t be as tricky as the Skyscraper version, at least once you get going!).
I’ve also decided to make Consecutive Sudoku the ‘puzzle of the month’ (”Masterclass”) puzzle in Sudoku Pro issue 45, which should be out in just under 2 months I think. Hopefully I’ll also make a book of them available online soon(ish!).
The rules for this Consecutive Samurai are simple: place 1 to 9 into each row, column and bold-lined 3×3 box of each of the 5 Sudoku grids, whilst also obeying the consecutive constraints – numbers with a white bar between are consecutive, whilst those without a white bar between are not consecutive. ”Consecutive” means that the difference between the values in the two squares is exactly 1: i.e. 1&2, 2&3, 3&4, 4&5, 5&6, 6&7, 7&8 or 8&9.
Good luck!
Shape Sudoku
Apr 23rd
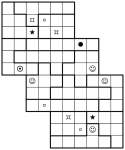
3-grid Shape Jigsaw Sudoku Samurai Stack
I needed to create one of these for a project elsewhere, so I thought I would post a couple of them here too – since I’d gone to the effort to make one at all! It’s not a new Sudoku variation, but just a very simple replacement of the digits 1 to 6 with shapes. None the less, it does make the puzzle notably harder to solve (or maybe that’s just me!). Unless there’s demand I won’t post this variant again, but I thought it would make an interesting change just for once!
I’ve created two examples – one is a simple 6×6 jigsaw, and the other is a 3-grid 6×6 Samurai Stack. In each case place one of each symbol into each 6-square row and column of each underlying 6×6 grid, and also one of each symbol into all of the bold-lined jigsaw shaped pieces.
Good luck!
5-grid Samurai Skyscraper
Apr 20th

Samurai 5-grid Skyscraper puzzle
I thought I’d try one more Skyscraper Samurai Sudoku puzzle – this time a 5-grid variety, or what I think of as the ‘traditional’ Samurai Sudoku format (some people also call this Gattai-5, but I’ve not seen that in print anywhere).
The aim is to place 1 to 9 into each row, column and 3×3 bold-lined box of each of the 5 9×9 Sudoku grids, whilst also obeying the Skyscraper constraints. These tell you the number of digits that can be ’seen’ from the edge of the grid looking in along the adjacent row/column, where higher numbers obscure lower ones. Take a look at a couple of last week’s puzzles if you need more detailed instructions for this constraint.
As has been pointed out in the comments elsewhere, it doesn’t matter whether you consider that the Skyscraper clues apply to the nearest 9×9 grid or to the entire width/height of the row/column they attach to – once the first ‘9′ is reached then there are no higher numbers, and that’s guaranteed to happen within the first 9 squares.
I think this is probably about as large as you want to go with a relatively complex constraint such as Skyscraper, which is why I’ve included quite a few given numbers too – including some which clearly aren’t needed to give the puzzle a unique solution. (But please tell me if I’m wrong about this being big enough – I could always make a much larger one still just to prove that it’s possible!)
This week I plan to try out some other types of consecutive Sudoku variant – there are a couple of moderately-well-known types where you specify certain relationships between adjacent squares, such as ‘x2′ (where one number is twice the adjacent one – a bit like a slightly less-constrained version of consecutive sudoku!). If you have any ideas for other variants, feel free to let me know – I might try them out!
Good luck!


Recent Comments