Skyscraper
Skyscraper Puzzles
Apr 28th
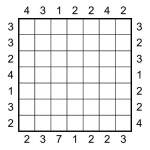
Skyscraper 7×7 puzzle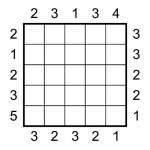
Skyscraper 5×5 puzzle
It occurs to me that I haven’t yet posted a regular, vanilla Skyscraper puzzle, so I decided that today was the day to rectify that! The 5×5 puzzle attached is pretty easy – it can be solved in under a minute if you’re on your toes! The 7×7 is nowhere near as hard as many of the puzzles I’ve posted recently, but it will certainly take longer than that.
The rules are simple: place 1 to 5 (or 1 to 7) into each row and column whilst obeying the skyscraper constraints. In Skyscraper puzzles each number in the completed grid represents a building of that many storeys, so the aim is to place the buildings in such a way that each given number outside the grid represents the number of buildings that can be seen from that point, looking along the adjacent row/column. A building with a higher value always obscures a building with a lower value, and a building with a lower value never obscures a building with a higher value. (Click back and look at some of my older posts for more details and examples)
Also, I want to say thanks very much for all of the fantastic comments that have been posted in response to my other puzzles – I’ve read them all and taken note and am working on suitable puzzles to follow up! ![]()
5-grid Samurai Skyscraper
Apr 20th

Samurai 5-grid Skyscraper puzzle
I thought I’d try one more Skyscraper Samurai Sudoku puzzle – this time a 5-grid variety, or what I think of as the ‘traditional’ Samurai Sudoku format (some people also call this Gattai-5, but I’ve not seen that in print anywhere).
The aim is to place 1 to 9 into each row, column and 3×3 bold-lined box of each of the 5 9×9 Sudoku grids, whilst also obeying the Skyscraper constraints. These tell you the number of digits that can be ’seen’ from the edge of the grid looking in along the adjacent row/column, where higher numbers obscure lower ones. Take a look at a couple of last week’s puzzles if you need more detailed instructions for this constraint.
As has been pointed out in the comments elsewhere, it doesn’t matter whether you consider that the Skyscraper clues apply to the nearest 9×9 grid or to the entire width/height of the row/column they attach to – once the first ‘9′ is reached then there are no higher numbers, and that’s guaranteed to happen within the first 9 squares.
I think this is probably about as large as you want to go with a relatively complex constraint such as Skyscraper, which is why I’ve included quite a few given numbers too – including some which clearly aren’t needed to give the puzzle a unique solution. (But please tell me if I’m wrong about this being big enough – I could always make a much larger one still just to prove that it’s possible!)
This week I plan to try out some other types of consecutive Sudoku variant – there are a couple of moderately-well-known types where you specify certain relationships between adjacent squares, such as ‘x2′ (where one number is twice the adjacent one – a bit like a slightly less-constrained version of consecutive sudoku!). If you have any ideas for other variants, feel free to let me know – I might try them out!
Good luck!
Skyscraper Jigsaw Samurai Sudoku
Apr 16th
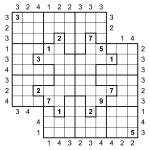
Skyscraper Jigsaw Samurai Sudoku puzzle
I’m pretty confident that you won’t have come across one of these puzzles before – I certainly haven’t! It’s a Samurai Skyscraper Sudoku puzzle with Jigsaw regions instead of regular 3×3 boxes.
The aim is to place 1 to 9 into each row and column of each of the two overlapping 9×9 grids, and also place 1 to 9 into each of the bold-lined jigsaw pieces. On top of that, you must also obey the Skyscraper constraints, which are the numbers outside the main puzzle grid. They specify the number of digits you can ’see’ from each point, where higher digits obscure lower digits (so a 7 obscures 1 to 6, and a 9 obscures all other digits, for example) – see yesterday’s post for a slightly longer explanation of how these constraints work.
Good luck!
Skyscraper Consecutive Sudoku
Apr 15th
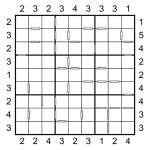
Skyscraper Consecutive Sudoku puzzle
Many of the best Sudoku variations can be combined with other variations in order to produce yet more types of puzzle. One variety I’ve personally never seen is to combine Skyscraper and Consecutive Sudoku together, so I thought I’d try it out today!
Skyscraper puzzles themselves are pleasant little puzzles where you must place 1 to 7 (or smaller) into each row and column of a grid whilst obeying ‘building height’ constraints around the edge. There’s an example 7×7 puzzle on this page over at puzzlemix. These building height constraints specify the number of notional buildings you could see whilst standing at the edge of the puzzle and looking in, whereby a taller building completely hides the view of any shorter building. The idea is that a digit ‘1′ in the grid is a building 1 storey high; a digit ‘2′ in the grid is a building 2 storeys high, and so on.
If you have a very simple 3×3 Skyscraper puzzle, here’s the potential solutions to each of the possible clues:
- 1: can be either 3 2 1 or 3 1 2, with the ‘3′ hiding both the other digits
- 2: can be 1 3 2 or 2 3 1 or 2 1 3.
- 3: can only be 1 2 3 because this is the only way to see all of the buildings.
I think that the maximum size of Skyscraper puzzle you can make without using any pre-solved numbers (givens) is 7×7, but by combining it with additional Sudoku constraints (i.e. the 3×3 boxes, and some given numbers in the puzzle already) you can make much larger puzzles.
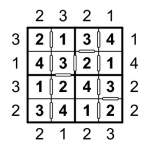
Example Consecutive Sudoku Skyscraper solution
So what we have here is a Skyscraper Sudoku – you must place 1 to 9 into each of the rows, columns and bold-lined 3×3 boxes whilst obeying the Skyscraper building height constraints around the edge of the puzzle. And then just to add an extra twist further to the puzzle, I’ve also included consecutive/non-consecutive constraints as in the previous days’ puzzles – click here for full instructions for these, but the basic idea is that a white bar separates two squares that have consecutive values (i.e. the mathematical difference is 1, so specifically 1&2, 2&3, 3&4, 4&5, 5&6, 6&7, 7&8 or 8&9) and if there’s no white bar then the difference is greater than 1 (i.e. they’re not consecutive).
I’ve attached an example 4×4 puzzle so you can be sure you understand how the Skyscraper (and consecutive) constraints work with this type of puzzle.
Good luck!

Recent Comments