Sudoku Variants
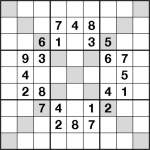
Samurai Star XXXXX
Mar 12th
I haven’t posted a puzzle for a week (it’s been a busy week, mind!) so it’s time to make up for that, just in time for the weekend.
In this puzzle the aim is pretty simple: place 1 to 9 in each set of 9 squares starting and ending with a bold line, whether in a row or column, and similarly for each set of 9 squares starting and ending with a bold line in any of the shaded diagonals.
Good luck! 
Killer Sudoku-X
Mar 4th
I wrote quite a lot yesterday about whether you “needed” the X in some Sudoku-X puzzles. I promised that I’d follow up with the result of analysing a stack of Killer Sudoku-X puzzles, and so here is that result.
I picked 64 Killer Sudoku-X puzzles (52 for the daily puzzlemix section plus 12 for the weekly puzzlemix section), and of those about 5 or 6 (I didn’t write it down…) could be solved via reasonable logical deduction without using the ‘X’ diagonals. So that’s roughly 10% of puzzles, if picked at random, that don’t need it. Quite a bit worse than regular Sudoku-X (see previous post), but nowhere near as high a percentage as I’d expected – I had thought it could be 50% or more, although I should say that this isn’t actually a fair comparison because I disabled the cleverest maths-solving techniques from my analysis software. So in fact this is comparing clever Sudoku-X solving against the same Sudoku-X solving with the addition of relatively less clever Killer Sudoku-X solving, so perhaps this biased the result much more to the non-Killer result (from yesterday) than it should have done. But anyway, I’m not writing a scientific paper and it’s good enough for me!
Killer Sudoku-X puzzleSo the result of all this is pretty simple: the Killer Sudoku-X on PuzzleMix for the coming year should be better than ever! You should need that X every time…
PS Enjoy the Killer Sudoku-X I’ve attached here! Just place 1 to 9 in each row, column, 3×3 box and main diagonal, plus make sure the cages add to the given amounts – and don’t repeat a number in a cage.
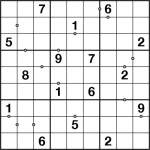
Sudoku-X and the diagonal challenge
Mar 3rd
One of the perennial comments on PuzzleMix is that the diagonal ‘X’ regions aren’t needed in a particular Sudoku-X puzzle, or more commonly in Killer Sudoku X. Well, when I say “perennial” I mean to say that of the more than 400,000 puzzle plays that that comment has been made about 10 times. But an interesting point nonetheless.
Obviously a regular Sudoku has 9 rows, 9 columns and 9 boxes. Are we annoyed if we don’t “need” all 27 regions? Probably not. But in an ‘X’ puzzle I suppose it’s understandable that you’d expect to use the ‘X’.
Now of course there are different definitions of “needing” a region. Strictly-speaking, if you can prove a unique solution via any method (e.g. recursive search) without the regions then you don’t need them. But I decided to define “need” as meaning “you can’t solve the puzzle without them whilst using the standard solving techniques”. Standard techniques are those that Nikoli allow, so everything up to x-wings and hidden/naked quads.
Using this definition I looked at 100 randomly-selected Sudoku X puzzles of mine and found that 98 “needed” the diagonals, and only 2 didn’t. Not bad! Of course this result will vary depending upon how vigorously you prune the number of ‘given’ digits in a puzzle.
It’s worth noting that not “needing” a region does not preclude it being useful – for example an easy Sudoku-X puzzle may happen to also be a very difficult regular Sudoku, so there is still value in including the regions even if they aren’t strictly-speaking essential. However there are enough Sudoku puzzle possibilities in the world that we can ignore this and simply select puzzles that don’t have any ambiguities.
So to celebrate, here’s a Sudoku X to solve. Just place 1-9 in each row, column, 3×3 box and the two main diagonals… but you know that already!
Next time I will look at Killer Sudoku X, but with the much heavier constraint of all the extra Killer regions I imagine the X will be needed far less of the time, thus the PuzzleMix comments. So I will be filtering my puzzles in future to make sure the X is always needed! I’ll also be filtering them for extra regions puzzles to make sure those are essential to solving them too.
Mind you, at the end of the day some people always find some puzzles easier than average just by making a fortuitous error – I’m sure we’ve all done it without realising! At those times there will always be puzzles that don’t seem to “need” the X…
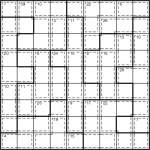
Jigsaw Killer Sudoku
Mar 2nd
I’ve recently been working on refreshing the content for PuzzleMix.com, my play-online puzzle site, and one of the puzzle types I’ve been making is Killer Jigsaw Sudoku, where you not only have the jigsaw-shaped Killer regions but also jigsaw shapes instead of the regular 3×3 Sudoku boxes.
So I thought it would be a good idea to post one of these puzzles here – they can be quite tricky, at least until you get your head around the difference between these and regular Killer!
The rules are simple:
- Place 1 to 9 in each row, column and bold-lined region
- Place numbers in the dashed-line cages that add up to the given total for that cage
- No number can be repeated in a dashed-line cage
Good luck!
Samurai Odd-Pair Sudoku
Mar 1st
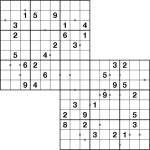
Samurai-2 Odd Pair Sudoku puzzle
One of the brand new puzzles in Sudoku Xtra issue 4 is Odd-Pair Sudoku, which I wrote about last week here on my puzzle blog. As well as some regular 9×9 puzzles I also included a large 5-grid Odd-Pair Samurai puzzle, and to illustrate how the puzzle worked I included a small solved example alongside. A full 5-grid Samurai was too big to fit sensibly in the example box, so I made a 2-grid Samurai version just for that little solution area. So that’s the solution used, but what about the puzzle itself? Well, here it is! (And so if you want to check your solution – yes, it’s printed in Sudoku Xtra issue 4! Page 19, to be precise).
The rules, in case you missed them, are really simple:
- Place 1 to 9 in each row, column and bold-lined 3×3 box of the two 9×9 Sudoku grids
- Every pair of squares with an ‘o’ circle between them must sum to an odd value. (’o’ for odd). So for example you could have “3 o 6″, but not “3 o 5″ (since that would sum to 8, an even number).
This variant is fun because it eliminates lots of possibilities from squares relatively quickly, so you’re left with more deductive logic and less pencil-mark housekeeping.
Good luck!
Sudoku Odd Pairs – a new variant!
Feb 23rd
Now here’s something I can guarantee you won’t have seen before, because I just invented it! Well, I suppose with a world of people creating Sudoku variants it’s possible there’s been something similar before, but I’ve bought a lot of puzzle magazines and books and never come across it, so perhaps I should say I can just about guarantee you won’t have seen it before!
So the puzzle is Sudoku Odd Pairs, and as the name implies it’s all about odd pairs of numbers. Now you may have come across regular odd/even Sudoku before, and to be honest it’s a pretty dull variant (which is why I’ve never made them) – in fact if you for example shade all squares that contain even numbers it just breaks into two separate puzzles that overlap, and if you instead mark just a selection of even (or odd) squares then it’s only interesting until you work out whether the shaded squares are odd or even.
Sudoku Odd Pairs isn’t like that, because instead of marking squares what I’ve done is mark pairs of squares. Some squares have a grey circle between them – you can think of this as an O for Odd. What this means is that the sum of the solution of these two squares is odd. I don’t mark all odd pairs, however, because if you do this you need only one single digit in the entire grid (any of the givens will do) to work out which squares are odd and which even and then you end up with the above boring variant again. So this is important: you can’t infer anything about squares without an O between them – only those with the O between.
It turns out (at least in my opinion!) that this is actually a really fun variant, because you end up with many interesting parts of each puzzle where you realise you can force sets of odds or evens into groups of squares (and not just those with the Os on), which in turn effect the rest of the puzzle. You do to an extent need to make pencil marks when solving, as in Consecutive and many other variants, but the nature of the constraint is such that the number of pencil marks is roughly halved relative to most other variants which (for me at least) makes it far more fun.
I’ve talked about it enough. Try out the puzzle here and let me know what you think!
And if you would like more of these, I’m putting them into Sudoku Xtra issue 4 (out soon!), including a nice Samurai version.
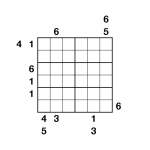
Outside Sudoku
Jan 14th
Here’s something new (for me at least) – an Outside Sudoku puzzle. This one’s 6×6, just to get the ball rolling, but I have some larger ones (including some Samurai ones) ready for Sudoku Xtra issue 3!
The numbers outside the grid reveal some, none or all of the numbers that go somewhere in that same row or column anywhere up to the first bold line encountered – in other words, they go in that row/column of the adjacent bold-lined region. If more than one number is given then the order need not necessarily be the same as that shown.
For example, look at the top-left. The 4 and the 1 both go somewhere in the first three squares of the top row, but not necessarily in that order. Below them the 6 goes in the first three squares of its row, and at the bottom-left of the puzzle the 4 and 5 go into the bottom two squares of the left-most column.
Then just follow through as a regular Sudoku until it is solved. Good luck!
Samurai Star Inequality
Dec 8th
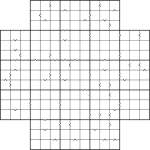
Samurai Star Inequality puzzle
I’m tempted to just say “good luck”, because frankly I think you’ll need it! Not of course in the literal sense, since this is an entirely logical problem, which requires absolutely no guess work, but in terms of finding the right areas to make progress quickly.
So having started at the end, let me introduce you to this Samurai Star Inequality puzzle. In all cases the “<” and “>” arrows point to the smaller number of each pair. Other than that it’s a regular Samurai Star – place 1 to 9 into each row, column and marked 3×3 box of each of the 5 underlying 9×9 grids (including the one in the centre).
And now back to the beginning: Good luck!
Inequality Sudoku
Dec 4th
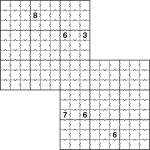
Inequality 2-grid Samurai Sudoku
Inequality jigsaw 6×6 Sudoku puzzle
On the Sudoku Xtra forums Marilyn suggested the great idea of an inequality Samurai puzzle for issue 2, so I’ve been having a look at doing this. And here’s the first result!
I’ve started off with a regular 6×6 jigsaw Sudoku, but have added inequalities, just to get you warmed up, then I’ve included my first ever Samurai Inequality Sudoku puzzle, albeit a 2-grid one for now.
You’ll notice in both puzzles here that I have included all inequality arrows, so you have far more information than you need – this is deliberate, to make them easier! On the 6×6 puzzle there are five really nice diamond shapes in the centre area, but in general I think having all the arrows is ugly (or lazy!) so I don’t plan to include them again in future (just as I’ve never included them in past published inequality/Futoshiki puzzles).
The rules of Inequality Sudoku are pretty simple – just place the numbers as you would in a regular Sudoku (or regular Jigsaw Sudoku in the 6×6 case), but obey the less-than (”<”) and greater-than (”>”) signs between squares. These indicate that the value of the number in a square is either less than or greater than its neighbour. And that’s it!
Good luck!
Stepping up – Three-away Sudoku!
Jul 21st
In a possibly inevitable next move (although in this case, I think, a probable conclusion to the theme rather than a stepping stone!) I thought I’d try out Three-away Sudoku, where black markers indicate all neighbouring squares with a difference of 3. With a 9×9 puzzle this still allows somewhat interesting 1-4-7, 2-5-8 and 3-6-9 chains to be used, although of course as you decrease the quantity of numbers that can fit in a chain so you start to lose the longer connected chains which I personally find so interesting.
Other than the three-away markers this is a regular 9×9 Sudoku puzzle, so just place 1 to 9 into each row, column and 3×3 box. Squares with a thick black bar between have a difference of 3 (e.g. 1&4), and those without a thick black bar between have a difference which is not 3.
An idea I have in mind to try next is to mix consecutive and two-away Sudoku in the same grid – I think any other combinations would be too confusing to play, although I suppose you could insert small numbers between squares to show selected differences which might make an interesting but possibly too mechanical variant. For me, I don’t want to have to stop and think about the rules I’m applying – in a good puzzle they should become intuitive really quickly (even if, in some cases, they are a little complex to learn they must become second nature for the puzzle to succeed – or so I find!).
Good luck!
Recent Comments