Sudoku
Non-Consecutive Sudoku
Mar 28th
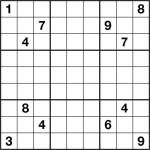
Non-consecutive Sudoku puzzleI’m currently working on a new book of sudoku variants for a major publisher, so have been making lots of new puzzles of different types. From time to time I’ll probably post again here with some examples of these.
I thought I’d start off with Non-Consecutive Sudoku. This is a minor variant on Consecutive Sudoku, where all the rules of standard Sudoku apply but there is one additional constraint:
- Neighbouring squares are not consecutive. This means there is never a difference of ‘1′ between two edge-adjacent squares (i.e. touching, not including diagonally).
For example, if a square contains ‘3′ then any neighbouring square cannot contain either ‘2′ or ‘4′.
Good luck!
Sudoku [Jigsaw] 6×6
Dec 7th
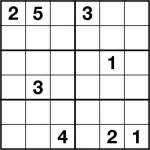
Sudoku 6×6 puzzle
Jigsaw 6×6 puzzle
I had a couple of 6×6 Sudoku puzzles left over when making issue 58 of Sudoku Pro magazine, so I thought I’d post them here.
Just place 1-6 into each row, column and bold-lined area.
Sudoku 16×16
Oct 14th
And to complement the Killer Sudoku I posted a moment ago, here’s a 16×16 puzzle for those who like these. Just place 1 to 9 and A to G in each row, column and 4×4 box. Only “scan and place” logic is needed for this, I promise!
Samurai 8X
Sep 6th
When I was making Sudoku Xtra 10 I wanted to put in a really big Samurai Sudoku puzzle. In the end because I had a square page area available beneath the instructions I went with a 13-grid one (just as a one-off to see what sort of reaction it got!) but I had started off intending to use an 8-grid one. It seemed a shame to let it go to waste, so I’m posting it here.
- Place 1 to 9 into each row, column, main diagonal and 3×3 box of each of the eight 9×9 grids.
- Note that, as in a regular Sudoku, only the rows, columns and main diagonals within the eight underlying 9×9 grids are guaranteed to contain all of 1-9. Any row, column or diagonal not entirely within a single 9×9 grid has no restriction on its content.
So best of luck – you don’t need it, but it might help anyway! ![]()
Samurai Killer Sudoku Pro 6×6
Apr 27th

Killer Sudoku Pro 6×6 Samurai puzzle
It’s been quiet here recently – much of my effort has been going on my UK General Election site, How To Vote, although Sudoku Xtra 6 was out on Saturday too. Anyway, there are still 10 days to go to the election but after that I’ll get some time back!
However I thought I should finally post another puzzle – so here one is. Place 1 to 6 in each row, column and 2×3 box (rows and columns are defined by the three underlying 6×6 grids, which you have to infer from the stepping). Also place numbers so that the value at the top-left of each dashed-line cage results from applying the operation between all the value in that cage. For subtraction and division start with the largest value.
Have fun! ![]()
Toroidal Killer Toroidal Jigsaw Sudoku
Mar 19th
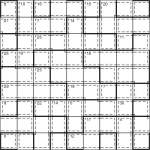
Toroidal Killer Jigsaw Toroidal puzzle
A while back someone asked for some variant toroidal patterns on PuzzleMix, so I was just adding a couple of them to the daily puzzles section when it occurred to me that I could put up a few toroidal killer sudoku too, for a change. However I then realised that the code which creates the HTML will need editing to cope with toroidal regions, but I knew my PDF code was more flexible… and then I thought it would be great to mix this with some toroidal jigsaw regions too… and here’s the somewhat confusing result! A Toroidal Killer with Toroidal Jigsaw regions.
Now if you enjoy this twisted beast let me know, otherwise I probably won’t make any more of them! ![]()
Full rules:
- Place 1 to 9 in each row, column and bold-lined jigsaw region
- Place numbers so that the dashed-line cages add to the total given
- No number can repeat in a dashed-line cage.
- Some jigsaw regions and cages ‘wrap around’ the outside the puzzle, continuing at the start/end of the same row/column
Good luck! ![]()
Samurai Star XXXXX
Mar 12th
I haven’t posted a puzzle for a week (it’s been a busy week, mind!) so it’s time to make up for that, just in time for the weekend.
In this puzzle the aim is pretty simple: place 1 to 9 in each set of 9 squares starting and ending with a bold line, whether in a row or column, and similarly for each set of 9 squares starting and ending with a bold line in any of the shaded diagonals.
Good luck! ![]()
Killer Sudoku-X
Mar 4th
I wrote quite a lot yesterday about whether you “needed” the X in some Sudoku-X puzzles. I promised that I’d follow up with the result of analysing a stack of Killer Sudoku-X puzzles, and so here is that result.
I picked 64 Killer Sudoku-X puzzles (52 for the daily puzzlemix section plus 12 for the weekly puzzlemix section), and of those about 5 or 6 (I didn’t write it down…) could be solved via reasonable logical deduction without using the ‘X’ diagonals. So that’s roughly 10% of puzzles, if picked at random, that don’t need it. Quite a bit worse than regular Sudoku-X (see previous post), but nowhere near as high a percentage as I’d expected – I had thought it could be 50% or more, although I should say that this isn’t actually a fair comparison because I disabled the cleverest maths-solving techniques from my analysis software. So in fact this is comparing clever Sudoku-X solving against the same Sudoku-X solving with the addition of relatively less clever Killer Sudoku-X solving, so perhaps this biased the result much more to the non-Killer result (from yesterday) than it should have done. But anyway, I’m not writing a scientific paper and it’s good enough for me!

Killer Sudoku-X puzzleSo the result of all this is pretty simple: the Killer Sudoku-X on PuzzleMix for the coming year should be better than ever! You should need that X every time… ![]()
PS Enjoy the Killer Sudoku-X I’ve attached here! Just place 1 to 9 in each row, column, 3×3 box and main diagonal, plus make sure the cages add to the given amounts – and don’t repeat a number in a cage.
Sudoku-X and the diagonal challenge
Mar 3rd
One of the perennial comments on PuzzleMix is that the diagonal ‘X’ regions aren’t needed in a particular Sudoku-X puzzle, or more commonly in Killer Sudoku X. Well, when I say “perennial” I mean to say that of the more than 400,000 puzzle plays that that comment has been made about 10 times. But an interesting point nonetheless.
Obviously a regular Sudoku has 9 rows, 9 columns and 9 boxes. Are we annoyed if we don’t “need” all 27 regions? Probably not. But in an ‘X’ puzzle I suppose it’s understandable that you’d expect to use the ‘X’.
Now of course there are different definitions of “needing” a region. Strictly-speaking, if you can prove a unique solution via any method (e.g. recursive search) without the regions then you don’t need them. But I decided to define “need” as meaning “you can’t solve the puzzle without them whilst using the standard solving techniques”. Standard techniques are those that Nikoli allow, so everything up to x-wings and hidden/naked quads.
Using this definition I looked at 100 randomly-selected Sudoku X puzzles of mine and found that 98 “needed” the diagonals, and only 2 didn’t. Not bad! Of course this result will vary depending upon how vigorously you prune the number of ‘given’ digits in a puzzle.
It’s worth noting that not “needing” a region does not preclude it being useful – for example an easy Sudoku-X puzzle may happen to also be a very difficult regular Sudoku, so there is still value in including the regions even if they aren’t strictly-speaking essential. However there are enough Sudoku puzzle possibilities in the world that we can ignore this and simply select puzzles that don’t have any ambiguities.
So to celebrate, here’s a Sudoku X to solve. Just place 1-9 in each row, column, 3×3 box and the two main diagonals… but you know that already!
Next time I will look at Killer Sudoku X, but with the much heavier constraint of all the extra Killer regions I imagine the X will be needed far less of the time, thus the PuzzleMix comments. So I will be filtering my puzzles in future to make sure the X is always needed! I’ll also be filtering them for extra regions puzzles to make sure those are essential to solving them too.
Mind you, at the end of the day some people always find some puzzles easier than average just by making a fortuitous error – I’m sure we’ve all done it without realising! At those times there will always be puzzles that don’t seem to “need” the X… ![]()
Samurai Odd-Pair Sudoku
Mar 1st
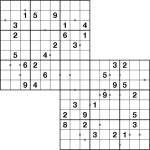
Samurai-2 Odd Pair Sudoku puzzle
One of the brand new puzzles in Sudoku Xtra issue 4 is Odd-Pair Sudoku, which I wrote about last week here on my puzzle blog. As well as some regular 9×9 puzzles I also included a large 5-grid Odd-Pair Samurai puzzle, and to illustrate how the puzzle worked I included a small solved example alongside. A full 5-grid Samurai was too big to fit sensibly in the example box, so I made a 2-grid Samurai version just for that little solution area. So that’s the solution used, but what about the puzzle itself? Well, here it is! (And so if you want to check your solution – yes, it’s printed in Sudoku Xtra issue 4! Page 19, to be precise).
The rules, in case you missed them, are really simple:
- Place 1 to 9 in each row, column and bold-lined 3×3 box of the two 9×9 Sudoku grids
- Every pair of squares with an ‘o’ circle between them must sum to an odd value. (’o’ for odd). So for example you could have “3 o 6″, but not “3 o 5″ (since that would sum to 8, an even number).
This variant is fun because it eliminates lots of possibilities from squares relatively quickly, so you’re left with more deductive logic and less pencil-mark housekeeping.
Good luck! ![]()



Recent Comments