Sudoku
Double Samurai Star
Jun 3rd
Following Spittledung’s comment on the Samura-i puzzle about it being nearly a double samurai star / flower samurai, I thought it would be fun to try out what exactly that would really look like – and so here is the result!
All of the 11 possible 9×9 grids are present, and you must place 1-9 into each row, column and 3×3 box of each of these underlying grids.
Good luck! ![]()
Samurai Square 9-grid
Jun 2nd
I was thinking about the tight overlay of grids in the (improved) Samura-I puzzles, and wondered what it would be like if you made a 15×15 puzzle simply by overlaying 9 Sudoku grids at all possible offsets. The answer is attached. This is definitely rated easy – there are lots of possible eliminations at all stages, and you shouldn’t need pencilmarks to solve it.
Of course, this principle can be extended to any arbitrary size of puzzle, but I imagine it would get a bit tedious if it was much larger…
So – can you place 1 to 9 into each row, column and 3×3 bold-lined box of each of the 9 underlying Sudoku grids in this puzzle? You’ll need to solve all 9 grids simultaneously to reach the solution.
Good luck! ![]()
New improved Samura-i
May 30th
I decided that I didn’t like the inelegance of having 3 grids across the top and bottom but not 3 grids down the centre column in yesterday’s Samurai-I, so I’ve fixed this for today’s puzzle – it’s pretty much the same except that now there are 9 grids here, at all possible bold-line offsets.
So can you place 1 to 9 into each of the rows, columns and bold-lined 3×3 boxes of the 9 grids in this Samurai-I puzzle?
Good luck! ![]()
Samura-i
May 29th
Here’s a new layout of Samurai Sudoku – a Samura-i, or Samurai I if you prefer! There are 7 grids here – 3 each at the top and bottom and then one in the middle too. Place 1 to 9 into each row and column of these 7 grids, as well as 1 to 9 into each bold-lined 3×3 box.
Just to re-emphasise this, there are no grids with top-left corner at offset 3 across, 3 down or at 3 across, 9 down. There’s just the absolute centre grid and then the top row and bottom row of 3 grids each. (Maybe this is a bit confusing – feel free to comment if you think so!)
Good luck! ![]()
Toroidal Sudoku
May 28th
Sorry for the lower quantity of puzzles this past week – I’ve been working on completing a new book so I’ve had to focus on that instead, but next week I’ll hopefully get back up to my five-a-week average! I’m not feeling very inspired in terms of being too original right now so I thought I’d post a ‘regular’ 9×9 toroidal Sudoku, although this one is a little tricky through having only 14 given numbers to start from!
As my easy and hard puzzles attest, I’ve been doing a lot of work on really accurately rating Sudoku puzzles, something which I’ve only done in a more general way before on the basis of what logic was necessary to solve a puzzle – now I can do a much more detailed analysis of the number of simultaneous possible moves at any stage of solving the puzzle, what those moves are, and at what point in the solve process they’re required. I needed this new accuracy of rating for one of my new books that will be out later this year (actually pretty soon, at the start of July), shown left – Hard-as-Nails Sudoku. It has over 200 really-difficult puzzles – they start out tricky (more than 10 minutes to solve) and end up… well, even harder than the tough puzzle I posted last week! But at no point do they use any ‘unfair’ solving logic – they stick fair and square to logic that any solver could come up with themself, without help. And of course, no guessing is ever required.
Anyway, it doesn’t take a complex analysis to see that today’s toroidal is not going to be on the easy side, given the low number of givens and the fact that toroidal puzzles really do twist things up in a difficult kind of way – so good luck! ![]()
The opposite of difficult
May 27th
After last week’s very difficult Sudoku, I thought it would be fun to try the complete opposite – an extremely easy Sudoku! At all stages of this puzzle there are lots of possible places to go, which means that your target time to beat (if you care to try) is two and a half minutes.
If you’re interested, I solved it in 2:13 but that included correcting for a careless mistake where I added two ‘4’s to one of the boxes! I’m probably twice as slow as the world’s best solvers so whilst I’m certain some of them could manage it in under a minute, I think anyone who manages it in under 2 minutes should be very proud!
Of course, it’s just for fun and if you have an off day it could take you as long as 3 minutes….. ![]()
Good luck! ![]()
Samurai Star
May 23rd
You might be pleased to know that today’s puzzle is somewhat easier, despite being a lot bigger! It’s actually possible to comfortably solve this without making a single pencilmark, if you fancy an extra challenge. ![]()
It’s a Samurai Star / Flower Samurai puzzle. Just place 1 to 9 into each row, column and 3×3 box of the 5 underlying grids (there’s one in the centre too).
Good luck!
Just a Sudoku… how hard do you find it?
May 21st
Following yesterday’s theme of scaling back to simpler puzzles, here’s a plain and simple Sudoku.
It might not be an unusual type of puzzle, but it’s interesting to me because I’m trying to calibrate the difficulty of tougher puzzles whilst avoiding solving strategies that casual solvers won’t know – I don’t want to make difficult puzzles simply by requiring obscure logic! (There’s nothing wrong with that in itself, but it’s not what I’m trying to do here). I’ve never put much effort into making really hard puzzles, mainly because it’s a minority interest and it’s not one I personally share too much (I like to get stuck, but not for too long! ![]() ). In general I’d rather my puzzles be tricky because they’re unfamiliar or are novel in some way.
). In general I’d rather my puzzles be tricky because they’re unfamiliar or are novel in some way.
Anyway, after a few easy placements this puzzle gets quite hard to make progress on – or so I think. I’d really, really like to hear how difficult (or not!) you find this puzzle, and how long it takes you to solve it. (I’ve also added it to puzzlemix.com if you’d like to play it online).
Thanks, and good luck! ![]()
Samurai Sudoku
May 20th
I thought it would be nice to have just a regular puzzle for a change – so today’s Sudoku is a standard, vanilla 5-grid Samurai Sudoku, without any twists!
Just place 1 to 9 into each row and column of the 5 underlying 9×9 grids, and 1 to 9 into each of the bold-lined 3×3 rectangles.
Good luck! ![]()
Wrap-around Consecutive 3-grid 6×6 Samurai Skyscraper
May 18th
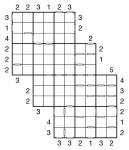
Wrap-around Consecutive 3-grid 6×6 Samurai Skyscraper puzzle
Another mouthful of a puzzle name, but in essence simply a development of the previous puzzle I posted. This time we still have the wrap-around consecutive-ness, but I’ve extended it to a samurai puzzle and added in skyscraper clues. To keep it reasonable, I’ve reduced the underylying Sudoku size to 6×6, however!
What’s particularly fun about the wrap-around markers is that they warp from one side of the puzzle to the same row/column on the opposite side – for the centre two columns this means that they constrain the values of two numbers 10 squares apart.
So the full rules are:
- Place 1 to 6 into each row, column and 2×3 bold-lined box of each of the three underlying 6×6 grids
- White bars show that adjacent cells are consecutive – i.e. 1&2, 2&3, 3&4, 4&5 or 5&6; those squares without a white bar between are non-consecutive
- White bars are shown where appropriate even on the edges of the grid – they indicate how the cell relates to the square at the far end of this row/column of numbers. Remember that the lack of such a white bar means that these wrap-around squares are non-consecutive.
- Skyscraper clues reveal how many numbers can be ’seen’ from that clue number counting in along the adjacent row/column, where higher numbers obscure all lower numbers (see previous puzzles for more detailed instructions)
Just to clarify, if adjacent numbers are equal (which is possible if they’re at far sides of the grid from one another) then these count as non-consecutive.
Good luck! ![]()







Recent Comments