Sudoku
Consecutive Sudoku
Apr 13th
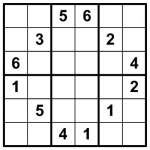
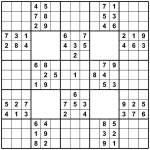
Standard Sudoku 6×6 puzzle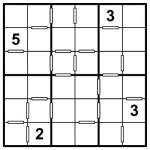
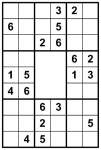
Consecutive Sudoku 6×6 puzzle
A Sudoku variant that I have always wanted to create, but somehow have just not quite ever got round to actually doing, is Consecutive Sudoku.
In Consecutive Sudoku, hollow bars between squares indicate that those two squares contain consecutive values – that is, each square is either one higher or one lower in value than the other. So if a square contains ‘3′ and there is a hollow bar between it and another square then that other square must contain either ‘2′ or ‘4′ – this is the consecutive constraint.
What makes it even more interesting is that the converse also applies – if there is not a hollow bar then the neighbouring squares are not consecutive. Therefore if a square contains ‘3′ then any neighbouring square without a hollow bar between them cannot contain either ‘2′ or ‘4′.
It might sound slightly complicated, but in fact the real beauty of this Sudoku variant is that it is actually beautifully simple when you come down to actually trying it. And what’s more, puzzles turn out to be considerably easier than you might imagine – the consecutive constraint is simple enough to trace and follow that it really helps you solve the puzzle, rather than being a complex relationship that just adds to the solving difficulty!
You also get the chance to use some new logic – it’s a very little bit like Futoshiki or Inequality Sudoku, but with (to me) a cleaner, more elegant solving path.
I’ve made an example puzzle. It’s 6×6 because it makes it easier to follow the rules if you’re new to the type – I’ll post some much larger versions soon, I promise!
Attached to this post are two puzzles, each leading to the same solution. The first is a (rather attractive circular) regular 6×6 Sudoku, which will give you the solution pretty easily if you need some help. The other is the consecutive version of the puzzle. As you can see, it has far less givens – just 4! But this is all that is needed. It shouldn’t take more than a few minutes to solve, I promise.
Standard Sudoku rules apply – place 1 to 6 into each row, column and 2×3 bold-lined box.
Good luck!
PS Just in case it isn’t obvious, when you click on the puzzle graphics they will open and load into a PDF viewer such as Adobe Acrobat (if you don’t have it click here to get it).
PPS And if you want to comment – e.g. say if you like this sort of puzzle and want to see more, or comment on how long it took you to solve it/how easy it was, then click on ‘No comments’ at the top of this post, or just click on the post title itself to open it in a new window with comments and comment box included.
Jigsaw Gap Samurai
Apr 12th
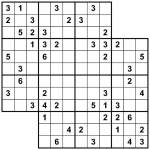
This is an interesting puzzle! It’s similar to yesterday’s Gap Samurai puzzles, except that the 3×3 box regions have been replaced by jigsaw regions – and not only that, but also some of these regions stretch across the empty areas of the puzzle.
The rules are:
- Wherever you see a continuous row or column of 9 squares from a bold line to a bold line then you must place 1 to 9.
- Rows or columns that cross gaps have no restrictions (numbers can repeat on the other side of the gap).
- Jigsaw regions must also have 1 to 9 in. Those jigsaw regions without bold lines next to a gap continue on the other side of the gap, by following a direct line across the gap. They do not flow around to the left or right, but only straight across. (If you’re familiar with Toroidal Sudoku, the regions connect in a similar way, except without actually wrapping around the outside of the puzzle too).
Confused? It isn’t actually that complex in concept, but keeping track of all the regions when solving might require a clear head! You might find it easier if you lightly colour in the different cross-gap regions in different colours in order to help keep track of them. (Sorry I haven’t coloured the PDF – I eventually will for future puzzles!)
If you’re still confused, and to clarify the regions further, count 4 across and 2 squares down from the top-left of the puzzle. This jigsaw region continues into the square below (obviously) and then across the gap to the square four below that (i.e. cross the gap whilst staying in the same column). It does not continue around the corner into the square that is 3 across by 4 down from the top-left – that’s part of a different region that continues in the centre of the puzzle (where the ‘8′ is, 8 across by 4 down). Returning to the first region, it then continues down to the ‘3′, and the ‘9′ and blank square to its right, and then down to the next square, across that second vertical gap, and then finishes in the two squares directly below (so that’s 4 across and 2/3 up from the bottom-left corner).
Phew! Good luck!
PS None of the Samurai puzzles I’m posting require complex solving logic – just an organised approach! (So you don’t need to consider naked or hidden sets, or anything more complex, although of course they might occasionally help anyway – but you can solve these puzzles without them).
PPS If you want to see solutions for any puzzles, just post a comment and ask! Also if you’ve solved one, please let me know how long it took – I’m interested to know!
Gap Samurai Sudoku
Apr 11th
I thought it would be interesting to try creating Samurai puzzles with gaps in, but to do this not just by creating an enormous puzzle but by putting gaps actually into the underlying Sudoku grids, so some rows and columns are incomplete.
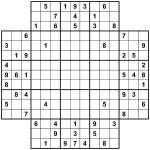
Take a look at the 6×9 puzzle attached (”2-grid 6×6 Samurai Gap puzzle”). Can you place 1 to 6 into each unbroken row and each bold-lined 2×3 box, whilst placing 1 to 6 into the top 6 and bottom 6 squares in each unbroken column? In other words, there are no rows or columns where there is a gap in the puzzle – you can repeat numbers on opposite sides of the gap.
This smaller puzzle is actually very easy, so I tried making a larger one with four 3×3 boxes ‘punched out’ of the puzzle. Again, where rows/columns run across the gaps then there are no restrictions on numbers repeating. Everywhere you find a continuous run of 9 squares from a bold line to a bold line in a row or a column then you must place all of 1-9 into that region. Also all of the 3×3 bold-lined boxes must contain 1 to 9 as usual.
In summary:
- Any continuous run of 9 squares starting on a bold line must have 1-9 in it, but
- Where a run of squares reaches a blank area then there are NO restrictions on that run – rows or columns don’t run across the gaps, in other words.
Incidentally, it would be perfectly reasonable for the rows/columns to continue across the gaps, but they don’t in these two puzzles – maybe they will in tomorrow’s puzzle! (it’s the obvious thing to change after all).
Repeated Digit Samurai Sudoku
Apr 10th
Here’s an interesting Samurai Sudoku variant. There are two 9×9 grids densely overlaid, so they share four of their 9×9 boxes in common – and not just this, but the numbers to place are one “1″, two “2″s, three “3″s and then one each of 4, 5 and 6.
In other words, can you place 1, 2, 2, 3, 3, 3, 4, 5, 6 into each row, column and 3×3 box of each of the two underlying 9×9 grids?
It might take a bit of getting your head around to start with, but it’s definitely do-able! Good luck!
Samurai Star
Apr 9th
One of my favourite Samurai Sudoku arrangements is the Samurai Star, also sometimes known as Flower Samurai. There’s been one every month in Sudoku Pro magazine for years, and what’s great about them is that because of the tight overlap of the underlying 9×9 grids there is some ‘new’ logic you can apply – essentially if a number occurs in a 3-cell row or column within a 3×3 box then that same number must also occur in the 3-cells that start 9 to the right/left/above/below (depending on whether it’s a 3-square row or column). It might sound confusing but it’s much more obvious when you try it out on an actual puzzle, and it’s one of those things that makes you go “ah, that’s nice” as you solve a puzzle – which is a good indicator of a decent design!
This particular puzzle has ‘8-way’ symmetry, which simply means that the pattern of givens is the same when reflected in both diagonals, and when rotated any multiple of 90 degrees, and when reflected and rotated.
The rules are simple: place 1 to 9 into each of the rows, columns and 3×3 boxes of the five underlying 9×9 Sudoku grids – four of them are obvious, and then there’s one in the centre too. It’s this centre grid that leads to the property I talk about above! You won’t find a unique solution if you omit this additional grid.
New puzzle blog
Apr 7th
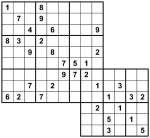
Samurai Sudoku 9×9 / 6×6 cross-over
I’ve decided it’s time to start posting puzzles online again, after a hiatus of about a year over on my old blog site.
I’m moving from my own bespoke blogging system to a standard one (WordPress), although it’s taken me a lot of effort to get PDF thumbnailing working! There doesn’t seem to be standard support for this, so I had to write my own PDF to thumbnail plug-in, which took a good few hours given that I knew nothing about WordPress – but anyway it now finally does work, so I can post my puzzles (like the attached) and get a decent thumbnail on the page too.
If that doesn’t make much sense, the basic point is that the small preview pictures like on the right will appear when I post puzzles automatically without me having to make each one by hand from the original PDF file. It also means when you click on them you’ll get a top-quality PDF ready for printing out at whatever size you like, rather than a fuzzy JPEG.
This puzzle is a 9×9 / 6×6 overlapping Samurai. The idea is to place 1 to 9 into each of the rows, columns and 3×3 boxes of the larger (top-left) grid, whilst placing 1 to 6 into each of the rows, columns and 2×3 boxes of the smaller (bottom-right) grid. Where they overlap there is a 3×3 box and a 2×3 box.
Good luck! It doesn’t need any tricky logic so shouldn’t be too taxing. Please do post a comment here if you like it, don’t like it, or indeed have anything to say at all!

Recent Comments