Posts tagged Samurai
Samurai Sudoku
May 20th
I thought it would be nice to have just a regular puzzle for a change – so today’s Sudoku is a standard, vanilla 5-grid Samurai Sudoku, without any twists!
Just place 1 to 9 into each row and column of the 5 underlying 9×9 grids, and 1 to 9 into each of the bold-lined 3×3 rectangles.
Good luck! ![]()
Wrap-around Consecutive 3-grid 6×6 Samurai Skyscraper
May 18th
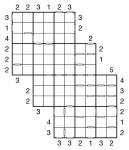
Wrap-around Consecutive 3-grid 6×6 Samurai Skyscraper puzzle
Another mouthful of a puzzle name, but in essence simply a development of the previous puzzle I posted. This time we still have the wrap-around consecutive-ness, but I’ve extended it to a samurai puzzle and added in skyscraper clues. To keep it reasonable, I’ve reduced the underylying Sudoku size to 6×6, however!
What’s particularly fun about the wrap-around markers is that they warp from one side of the puzzle to the same row/column on the opposite side – for the centre two columns this means that they constrain the values of two numbers 10 squares apart.
So the full rules are:
- Place 1 to 6 into each row, column and 2×3 bold-lined box of each of the three underlying 6×6 grids
- White bars show that adjacent cells are consecutive – i.e. 1&2, 2&3, 3&4, 4&5 or 5&6; those squares without a white bar between are non-consecutive
- White bars are shown where appropriate even on the edges of the grid – they indicate how the cell relates to the square at the far end of this row/column of numbers. Remember that the lack of such a white bar means that these wrap-around squares are non-consecutive.
- Skyscraper clues reveal how many numbers can be ’seen’ from that clue number counting in along the adjacent row/column, where higher numbers obscure all lower numbers (see previous puzzles for more detailed instructions)
Just to clarify, if adjacent numbers are equal (which is possible if they’re at far sides of the grid from one another) then these count as non-consecutive.
Good luck! ![]()
Consecutive Samurai CalcuDoku
May 5th

Consecutive Samurai CalcuDoku puzzle
Now this is an interesting puzzle! At first glance it looks like it can’t possibly have a unique solution, since there are no givens and only 9 cages on the entire 3-grid Samurai puzzle (made up of 6×6 grids). But in fact it uses only simple logic to solve, and it unravels pretty quickly once you get going. It’s a pretty powerful demonstration of how much you can strip a puzzle back and still keep it entirely reasonable in terms of difficulty. In fact it’s arguably too easy…
The rules are what you’d expect if you’ve been following previous puzzles, but in summary you must: (deep breath!)
- Place 1 to 6 into each row and column of the three underlying 6×6 grids
- Place numbers into each of the bold-lined cages so that they add up to the number at the top-left (or in the case of the 40x cage, multiply up to that value)
- Wherever a white bar divides two squares, the numbers in those two squares must be consecutive (so they must be one of these pairs: 1&2, 2&3, 3&4, 4&5 or 5&6)
- Where no white bar divides two squares, the numbers are non-consecutive
Good luck!
Samurai Star Killer Sudoku
Apr 29th
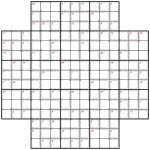
Samurai Star Killer (gentle) puzzle
“Star Killer” sounds like something out of science fiction, but it’s now definitely reality with this 5-grid Killer Sudoku puzzle. The actual Killer part uses the most basic logic imaginable, and there are a lot of ’singleton’ regions which I’ve never used in a Killer puzzle before. The reason for this is that I wanted to start at a gentle level – as a result this mostly solves like a regular Samurai Star (a.k.a. Flower Samurai) puzzle, with the Killer regions used occasionally to either get you going or help you out with a quick number along the way. It shouldn’t take you much over 20 or 30 minutes if you’ve solved this shape of Samurai before, and know what a Killer Sudoku is!
The rules are pretty simple: place 1 to 9 into each row, column and bold-lined 3×3 shape of each of the 5 underlying 9×9 grids (there’s one in the centre too), whilst also placing numbers so that the total in each dashed-line cage is equal to that given in the top-left corner. You may not repeat a number within a dashed-line cage.
The puzzle has rotation symmetry order 4, so the cages are in a pleasing pattern I hope – I particularly like the hole in the square in the centre! I think by and large that if you can create the cages or givens in a puzzle with the same order of symmetry that you have for the grid layout itself that this generally leads to a more pleasing appearance for the puzzle; but more than this, I find that this tends to follow through with the solving process, and you end up with pieces of the puzzle that feel ’sympathetic’ to one another, since the symmetry leads to related discoveries. However it’s perhaps not clear that this solving benefit carries through to a puzzle this large, and it’s probably the case that a puzzle with entirely random cages would feel just the same to actually solve at this size. But it wouldn’t look as nice!
Coming up in the following days I’m going to experiment in the space between Killer Sudoku and Ken Ken™ – in other words, using more operations than just addition, and possibly allowing repeated numbers in cages (although not on puzzles with 1-9 to place!). I already came across a puzzle called ‘Killer Sudoku Pro’ in the Saturday Telegraph newspaper (UK) – in this they keep the Killer Sudoku rules about not repeating digits in a cage, but specify different operations for cages (in actual fact the rules aren’t stated next to the puzzle in full, but I presume repeated digits are disallowed - it certainly solves okay with that assumption!). I haven’t seen anything precisely like that elsewhere and I thought it was actually quite fun (it wasn’t too hard!) so I’ll definitely try making some of those soon for sure. If you have any other ideas for how to mix these different types together feel free to post a comment!
Good luck!
Consecutive 5-grid Samurai Sudoku
Apr 24th
I thought it would be a nice idea to create a large Consecutive Sudoku for the weekend! And so here one is: a 5-grid Samurai Consecutive Sudoku. As you can see, there are very few givens to start with, so it will hopefully be at least a bit of a challenge! (It shouldn’t be as tricky as the Skyscraper version, at least once you get going!).
I’ve also decided to make Consecutive Sudoku the ‘puzzle of the month’ (”Masterclass”) puzzle in Sudoku Pro issue 45, which should be out in just under 2 months I think. Hopefully I’ll also make a book of them available online soon(ish!).
The rules for this Consecutive Samurai are simple: place 1 to 9 into each row, column and bold-lined 3×3 box of each of the 5 Sudoku grids, whilst also obeying the consecutive constraints – numbers with a white bar between are consecutive, whilst those without a white bar between are not consecutive. ”Consecutive” means that the difference between the values in the two squares is exactly 1: i.e. 1&2, 2&3, 3&4, 4&5, 5&6, 6&7, 7&8 or 8&9.
Good luck!
Shape Sudoku
Apr 23rd
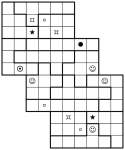
3-grid Shape Jigsaw Sudoku Samurai Stack
I needed to create one of these for a project elsewhere, so I thought I would post a couple of them here too – since I’d gone to the effort to make one at all! It’s not a new Sudoku variation, but just a very simple replacement of the digits 1 to 6 with shapes. None the less, it does make the puzzle notably harder to solve (or maybe that’s just me!). Unless there’s demand I won’t post this variant again, but I thought it would make an interesting change just for once!
I’ve created two examples – one is a simple 6×6 jigsaw, and the other is a 3-grid 6×6 Samurai Stack. In each case place one of each symbol into each 6-square row and column of each underlying 6×6 grid, and also one of each symbol into all of the bold-lined jigsaw shaped pieces.
Good luck!
5-grid Samurai Skyscraper
Apr 20th

Samurai 5-grid Skyscraper puzzle
I thought I’d try one more Skyscraper Samurai Sudoku puzzle – this time a 5-grid variety, or what I think of as the ‘traditional’ Samurai Sudoku format (some people also call this Gattai-5, but I’ve not seen that in print anywhere).
The aim is to place 1 to 9 into each row, column and 3×3 bold-lined box of each of the 5 9×9 Sudoku grids, whilst also obeying the Skyscraper constraints. These tell you the number of digits that can be ’seen’ from the edge of the grid looking in along the adjacent row/column, where higher numbers obscure lower ones. Take a look at a couple of last week’s puzzles if you need more detailed instructions for this constraint.
As has been pointed out in the comments elsewhere, it doesn’t matter whether you consider that the Skyscraper clues apply to the nearest 9×9 grid or to the entire width/height of the row/column they attach to – once the first ‘9′ is reached then there are no higher numbers, and that’s guaranteed to happen within the first 9 squares.
I think this is probably about as large as you want to go with a relatively complex constraint such as Skyscraper, which is why I’ve included quite a few given numbers too – including some which clearly aren’t needed to give the puzzle a unique solution. (But please tell me if I’m wrong about this being big enough – I could always make a much larger one still just to prove that it’s possible!)
This week I plan to try out some other types of consecutive Sudoku variant – there are a couple of moderately-well-known types where you specify certain relationships between adjacent squares, such as ‘x2′ (where one number is twice the adjacent one – a bit like a slightly less-constrained version of consecutive sudoku!). If you have any ideas for other variants, feel free to let me know – I might try them out!
Good luck!
Consecutive Samurai Star
Apr 17th
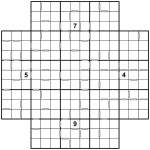
Samurai Star Consecutive puzzle
If the smaller consecutive puzzles weren’t enough of a challenge then this one should be! There are five overlaid 9×9 grids (including a ‘hidden’ one in the middle) which each need to have 1 to 9 placed into every row, column and bold-lined 3×3 box. On top of this you must obey the consecutive constraints – numbers with a white bar between are consecutive (12, 23, 34, 45, 56, 67, 78 or 89) and those without a bar between are not consecutive.
As you can see, the combination of tightly-overlaid grids and the consecutive marks means that very few givens are needed! Remember that none of these puzzles need ‘complex’ solving logic (you don’t need hidden or naked sets, X-wings or any other even more exotic strategy).
Good luck!
PS If there are any particular Sudoku or Samurai variants you’d like to see, please let me know and I’ll see what I can do!
Skyscraper Jigsaw Samurai Sudoku
Apr 16th
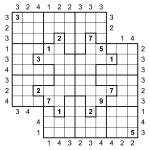
Skyscraper Jigsaw Samurai Sudoku puzzle
I’m pretty confident that you won’t have come across one of these puzzles before – I certainly haven’t! It’s a Samurai Skyscraper Sudoku puzzle with Jigsaw regions instead of regular 3×3 boxes.
The aim is to place 1 to 9 into each row and column of each of the two overlapping 9×9 grids, and also place 1 to 9 into each of the bold-lined jigsaw pieces. On top of that, you must also obey the Skyscraper constraints, which are the numbers outside the main puzzle grid. They specify the number of digits you can ’see’ from each point, where higher digits obscure lower digits (so a 7 obscures 1 to 6, and a 9 obscures all other digits, for example) – see yesterday’s post for a slightly longer explanation of how these constraints work.
Good luck!
Consecutive Samurai Sudoku
Apr 14th
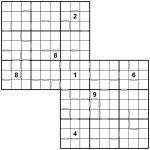
Consecutive 2-grid Samurai Sudoku
Well I promised a larger Consecutive Sudoku puzzle yesterday, and here one certainly is! It’s a 2-grid Consecutive Samurai Sudoku puzzle and the rules are essentially exactly the same as for yesterday’s puzzle except applied to a much larger grid.
The aim is to fit 1 to 9 into each of the rows, columns and 3×3 boxes of both of the two overlapping 9×9 puzzle grids, whilst obeying the consecutive constraints. In quick summary (read my full description yesterday), squares separated by a white bar contain values that are ‘consecutive’ – have a difference in value of exactly 1 – and those squares without a white bar between them are not consecutive – they have a difference in value greater than 1.
This puzzle is much trickier than my 6×6 example. It will probably take you half an hour or more to solve, of which by far the hardest part is working out how to start. Once you get going (which doesn’t require writing in ridiculous numbers of pencilmarks, I promise) it should keep flowing pretty smoothly.
If you need a hint then, the short version is this:
- You only have a few given numbers, so focus on areas around these – you don’t really need to worry about entirely empty parts of the grid far away from the givens to get going.
- Remember to solve both grids simultaneously and pay attention to the non-consecutive squares too!
- Focus on the centre 3×3 box – the information from both grids will help you make progress on it (and then from there you can actually consider both grids mostly independently)
A more detailed hint (but only a hint – not full instructions for getting going!) is this: after filling a few easy numbers around the ‘9′ in the bottom-right grid, the secret is to consider where a ‘9′ can go in the very centre box. Part of this deduction is remembering (and this is critical!) not just to pay attention to the consecutive squares but also the non-consecutive ones! Noting that the number directly below the ‘8′ in the centre 3×3 box of the top-left grid cannot possibly be a 7 or a 9 (and therefore the number to the right of that cannot be an 8, and the one to the right of that can’t be a 9) is a critical part of this process, along with a few deductions based around possible placements of 9s in the left three columns of the bottom-right 9×9 grid.
Good luck! (Once you get going this is a really fun puzzle!)



Recent Comments