Posts tagged Sudoku
Solving Sudoku using Robots!
Sep 2nd
Not a puzzle in itself, but I came across something related to Sudoku that’s so technically impressive that I just had to post about it.
There are plenty of online or interactive Sudoku solvers, and even some real-world ones which take the pages of a book, scan it in and then solve. SudokuGrab for iPod/iPhone is one popular example, whilst other people have used a combination of Lego and a webcam to scan in and solve entire books.
But how about this? A Sudoku solver robot which you can build yourself, and doesn’t even need a computer to drive it – it runs directly from a single Mindstorms Lego robotics kit. It’s unbelievable to watch it work, using a single point light sensor which the robot waves back and forth over the paper to build an image – there is no Lego webcam which can be integrated with the Mindstorms robotic kit. And then, as if it wasn’t already impressive enough, it uses a real pen to write in the solution.
It’s just amazing – take a look at the robot!
Stepping up – Three-away Sudoku!
Jul 21st
In a possibly inevitable next move (although in this case, I think, a probable conclusion to the theme rather than a stepping stone!) I thought I’d try out Three-away Sudoku, where black markers indicate all neighbouring squares with a difference of 3. With a 9×9 puzzle this still allows somewhat interesting 1-4-7, 2-5-8 and 3-6-9 chains to be used, although of course as you decrease the quantity of numbers that can fit in a chain so you start to lose the longer connected chains which I personally find so interesting.
Other than the three-away markers this is a regular 9×9 Sudoku puzzle, so just place 1 to 9 into each row, column and 3×3 box. Squares with a thick black bar between have a difference of 3 (e.g. 1&4), and those without a thick black bar between have a difference which is not 3.
An idea I have in mind to try next is to mix consecutive and two-away Sudoku in the same grid – I think any other combinations would be too confusing to play, although I suppose you could insert small numbers between squares to show selected differences which might make an interesting but possibly too mechanical variant. For me, I don’t want to have to stop and think about the rules I’m applying – in a good puzzle they should become intuitive really quickly (even if, in some cases, they are a little complex to learn they must become second nature for the puzzle to succeed – or so I find!).
Good luck! ![]()
Two-away Jigsaw 8×8
Jul 20th
Continuing with Two-away puzzles, I thought today I’d post a somewhat smaller challenge – an 8×8 Jigsaw Sudoku version.
The rules are pretty much what you’d imagine: place 1 to 8 into each row, column and bold-lined jigsaw piece. Numbers with a grey bar between them must have a difference of 2 (e.g. 1&3) and numbers without a grey bar between must have a difference that’s not 2. (This is important to ensure a unique solution!)
Good luck! ![]()
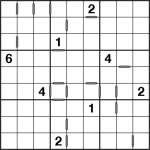
Two-away Samurai Jigsaw
Jul 17th
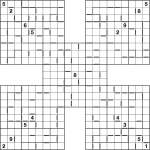
Two-away Samurai Jigsaw puzzle
Here’s a puzzle for the weekend – it’s a 5-grid samurai sudoku where in the corner grids a couple of the 3×3 regions have had their outlines tweaked to turn them into jigsaw sudoku puzzles, with full 8-way symmetry. There are very few givens, which means you’ll need to take full advantage of the two-away markers that are also in the grid. The grey rectangles indicate all neighbouring squares where the difference is 2 (e.g. 1&3 or 6&8) – even without precise values they can also be useful for quickly indicating where a chain of squares are all odd or all even.
Good luck! ![]()
Two-away Samurai Star
Jul 16th
I made this puzzle yesterday but then went and forgot to post it (oops) so I’m making up for that now! It’s a Samurai Star with two-away markers, just as per the previous two puzzles I posted.
Place 1 to 9 into each of the rows, columns and 3×3 boxes of the 5 underlying Sudoku grids (including the one in the centre), whilst obeying the two-away grey bars. Squares with a grey bar between have a difference of 2 (e.g. 1&3 or 2&4), and those without a grey bar have a difference which is not 2.
There are only 4 givens to get you going, so good luck! ![]()
Easy Two-away Sudoku
Jul 9th
I thought that yesterday’s puzzle wasn’t the best example of a new variant, so here’s an easier Two-away Sudoku puzzle. It has a few more connected squares which means the odd/even nature of the puzzle comes through a bit more clearly – if you’re familiar with consecutive sudoku then it probably won’t take you very long to solve.
The rules are as yesterday: place 1 to 9 into each row, column and 3×3 box, and then wherever a grey bar separates two squares the difference must be 2 – they must be “two-away” – and conversely where there is no grey bar then the difference is not 2.
Good luck! ![]()
Two-away Sudoku
Jul 8th
I just noticed that Monday marked my 50th post to garethmoore.co.uk, so to celebrate I thought I’d try a (slightly) new variation today: Two-away Sudoku. As its appearance might suggest, it is a close relative of Consecutive Sudoku. In fact it’s pretty much the same, except that the shaded grey bars indicate that the difference between neighbouring squares is 2 (not 1, as in Consecutive Sudoku). As in Consecutive Sudoku, all grey bars are drawn – so if one is absent then the difference is not 2.
For example, if you see a grey bar next to a square with ‘1′ in it then the neighbouring square must be ‘3′. However if you have a square with ‘1′ in and there is no grey bar between it and a neighbouring square then that square cannot contain ‘3′. It’s pretty simple really.
So – just place 1 to 9 into each row, column and 3×3 box whilst obeying the grey two-away markers!
Good luck! ![]()
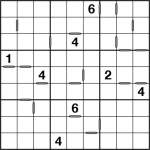
Wrap-around Consecutive Samurai Star
Jul 6th
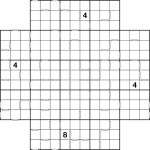
Wrap-around Consecutive Samurai Star puzzle
I seem to be posting more infrequently than I intend, so I thought I’d compensate with a puzzle that would take somewhat longer to complete! Here, then, is a wrap-around consecutive samurai star. All squares with consecutive values (a difference of 1) are marked with white bars, including those at opposite ends of rows and columns – wherever there isn’t a bar, the values are not consecutive.
The Sudoku logic takes a few twists here and there – in fact at one point near the end you will need to spot a particularly nasty hidden set in one region.
To solve the puzzle place 1 to 9 into each row, column and 3×3 box of each of the underlying 5 Sudoku grids (including the one in the centre). You’re only given 4 givens to get going, but with the consecutive information that’s all you need to find a unique solution.
Good luck! ![]()
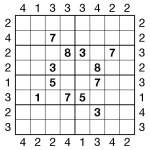
(Non-consecutive) Consecutive Sudoku 12×12
Jun 30th

Consecutive 12×12 Sudoku puzzle
After a bit of a break to meet a major book deadline – the non-consecutive part of the title of this posting – I’m back with what seems to be one of the most popular types of puzzle, a Consecutive Sudoku. I wanted something a little bit different, though, so this is a Consecutive Sudoku 12×12. I personally always find Sudoku 12×12 pretty similar to regular 9×9 Sudoku to solve, unlike something like 16×16 which personally I’d never really bother with (apologies to anyone who loves them!).
In order to make the consecutive nature of the 12 possible values obvious, I’ve used one- and two-digit numbers rather than digits and letters. So the rules are simple: place 1 to 12 into each row, column and 4×3 box whilst obeying the white consecutive markers. Wherever there is a white consecutive marker between two squares then the difference of value in those two squares is 1; and conversely whereever there is no marker the difference is always greater than 1.
So sorry for the break – hopefully ‘normal’ service will now be resumed! ![]()
And good luck with the puzzle!
Skyscraper Sudoku 8×8
Jun 19th
Continuing my series of 8×8 Skyscrapers and variants, here’s an 8×8 Sudoku with Skyscraper clues around the edge.
The rules are simple:
- Place 1 to 8 in each row, column and 4×2 box
- Obey the Skyscraper constraints: each number outside the grid reveals the number of ‘visible’ digits looking along that row/column, where higher digits obscure lower ones
Good luck!



Recent Comments