Posts tagged Sudoku
Just a Sudoku… how hard do you find it?
May 21st
Following yesterday’s theme of scaling back to simpler puzzles, here’s a plain and simple Sudoku.
It might not be an unusual type of puzzle, but it’s interesting to me because I’m trying to calibrate the difficulty of tougher puzzles whilst avoiding solving strategies that casual solvers won’t know – I don’t want to make difficult puzzles simply by requiring obscure logic! (There’s nothing wrong with that in itself, but it’s not what I’m trying to do here). I’ve never put much effort into making really hard puzzles, mainly because it’s a minority interest and it’s not one I personally share too much (I like to get stuck, but not for too long! ![]() ). In general I’d rather my puzzles be tricky because they’re unfamiliar or are novel in some way.
). In general I’d rather my puzzles be tricky because they’re unfamiliar or are novel in some way.
Anyway, after a few easy placements this puzzle gets quite hard to make progress on – or so I think. I’d really, really like to hear how difficult (or not!) you find this puzzle, and how long it takes you to solve it. (I’ve also added it to puzzlemix.com if you’d like to play it online).
Thanks, and good luck! ![]()
Samurai Sudoku
May 20th
I thought it would be nice to have just a regular puzzle for a change – so today’s Sudoku is a standard, vanilla 5-grid Samurai Sudoku, without any twists!
Just place 1 to 9 into each row and column of the 5 underlying 9×9 grids, and 1 to 9 into each of the bold-lined 3×3 rectangles.
Good luck! ![]()
Wrap-around Consecutive 3-grid 6×6 Samurai Skyscraper
May 18th
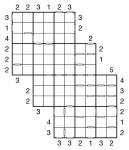
Wrap-around Consecutive 3-grid 6×6 Samurai Skyscraper puzzle
Another mouthful of a puzzle name, but in essence simply a development of the previous puzzle I posted. This time we still have the wrap-around consecutive-ness, but I’ve extended it to a samurai puzzle and added in skyscraper clues. To keep it reasonable, I’ve reduced the underylying Sudoku size to 6×6, however!
What’s particularly fun about the wrap-around markers is that they warp from one side of the puzzle to the same row/column on the opposite side – for the centre two columns this means that they constrain the values of two numbers 10 squares apart.
So the full rules are:
- Place 1 to 6 into each row, column and 2×3 bold-lined box of each of the three underlying 6×6 grids
- White bars show that adjacent cells are consecutive – i.e. 1&2, 2&3, 3&4, 4&5 or 5&6; those squares without a white bar between are non-consecutive
- White bars are shown where appropriate even on the edges of the grid – they indicate how the cell relates to the square at the far end of this row/column of numbers. Remember that the lack of such a white bar means that these wrap-around squares are non-consecutive.
- Skyscraper clues reveal how many numbers can be ’seen’ from that clue number counting in along the adjacent row/column, where higher numbers obscure all lower numbers (see previous puzzles for more detailed instructions)
Just to clarify, if adjacent numbers are equal (which is possible if they’re at far sides of the grid from one another) then these count as non-consecutive.
Good luck! ![]()
Consecutive Wrap-Around Sudoku
May 16th
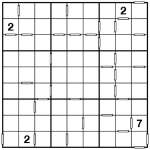
Consecutive Wrap-around Fiendish Sudoku puzzle
Here’s a slight twist on Consecutive Sudoku – I’ve included ‘wrap-around’ consecutive indication, where rows that start and end in consecutive digits have a white bar at the start and end of the row to show this, and similarly for columns. If they’re non-consecutive then there is no white bar. Similarly between all other squares: a white bar indiciates that two squares are consecutive, and no white bar means that they are non-consecutive.
‘Consecutive’ means that the difference between the numbers is ‘1′, i.e. they are 1&2, 2&3, 3&4, 4&5, 5&6, 6&7, 7&8 or 8&9. Other than this it’s a regular Sudoku – place 1 to 9 into each row, column and bold-lined 3×3 box.
This is also a difficult Sudoku, so if you can solve it under 20 minutes that would definitely be good going. Don’t forget about the non-consecutiveness – this is very important to reach the solution, and don’t forget about the wrap-around!
Good luck!
Double Toroidal Killer Sudoku Pro 8×8
May 13th

Double Toroidal Killer Sudoku Pro 8×8 puzzle
This puzzle certainly won’t be to everyone’s tastes, but it’s a double toroidal killer sudoku pro. Why double? Because there are toroidal jigsaw-shaped Sudoku regions, and there are toroidal jigsaw-shaped Killer Sudoku Pro cages. In other words, some of them wrap around the edges of the puzzle. It’s also an 8×8 puzzle, just to keep the Killer Sudoku (Pro!) logic fresh.
The rules are as you might expect:
- Place 1 to 8 into each row, column and bold-lined shape – some of these shapes are toroidal, so wrap from the end of one row/column to the opposite end of the same row/column
- Place numbers into the dashed-line Killer Sudoku Pro cages so that when the given operation is applied the result is the stated number. For ‘-’ operations start with the highest number.
- Numbers can’t repeat in dashed-line cages, and some cages (just one in this puzzle actually) are toroidal, so wrap around the rows/columns as described above
And that’s it! ![]() Good luck!
Good luck!
Hints: As always with this sort of puzzle, if you shade in the 8 bold-lined regions first with different colours you’ll find it much easier to keep track of what you’re doing. Also, all of the regions (both killer cages and bold-lined regions) have rotational symmetry order 4 – in other words, the same pattern repeats 4 times; this might help!
Toroidal Killer Sudoku 10×10
May 12th

Toroidal Killer Sudoku 10×10 puzzle
So far all of the “pure Sudoku logic” in my puzzles posted here has been pretty gentle. Well I decided that it was time to change that, but of course I wasn’t about to do that with a common garden puzzle! So I’ve applied some harder logic to this 10×10 Killer Sudoku with toroidal cages.
Because this is a 10×10 puzzle I’ve kept the Killer Sudoku part very easy – there are plenty of single cages (with apologies to those who dislike these!) and although the maths goes a tiny bit higher the actual ‘Killer reasoning’ is straightforward. But the Sudoku reasoning itself is definitely tougher, in places.
So here are the rules:
- Place 1 to 10 into each row, column and bold-lined 5×2 cage
- Place numbers so that they add up to the total at the top-left of each dashed-line cage
- Numbers may not repeat within a dashed-line cage
- Some cages wrap around the edges of the puzzle – they continue in the same row/column on the opposite side of the puzzle (so a cage leaving off the right of row 3 continues on the left edge of row 3, and vice-versa)
In summary, then, there are a few relatively unusual things here: the 1-10 Killer sums and 1-10 Sudoku; the toroidal cages; and the fact that this Killer requires tough Sudoku logic and so plays more like a 1-10 regular Sudoku than a 1-10 Killer… once you get going, that is!
Good luck! ![]()
Skyscraper Sudoku
May 11th
It occurs to me that I didn’t get round to posting any ’straightforward’ Skyscraper Sudoku puzzles previously, so I thought I’d rectify that today. Attached is a regular 9×9 Sudoku with the addition of Skyscraper clues around the edge, and no other twists!
For the Skyscraper clues the numbers around the edge represent the number of digits visible from that point looking in along the row/column, where higher digits obscure all lower digits. So for example the solution to the clue ‘9′ would have to be 123456789, otherwise you couldn’t see all 9 digits; if the clue is ‘1′ then the first digit must be a 9, hiding all of the other digits. However the solution to the clue ‘8′ might be 134567829, where the ‘2′ is “hidden” behind the higher digits, or one of several other possibilities. For more examples and more detailed instructions click back to some of my older puzzle postings.
On a completely different topic, if you’ve had any trouble viewing the most recent few puzzles then I apologise – it turns out that some of them wouldn’t open in older versions of Adobe Acrobat Reader (version 7 wouldn’t open them, at any rate – the current version is 9.1). I changed the way I make PDFs a week ago, but I hope I’ve now fixed what I think was causing the problem! If today’s puzzle won’t open for you I’d be incredibly grateful if you could post a comment and tell me what PDF viewer you’re using and what error message you get! ![]()
Good luck with today’s puzzle!
Samurai Toroidal Killer Sudoku Pro 13-grid
May 7th

Samurai Toroidal 13-grid Killer Sudoku Pro puzzle
Now this is a puzzle I can state with confidence that you won’t have seen before. It’s a Killer Sudoku Pro puzzle – i.e. a Killer Sudoku with -, x and / regions too; but more than that it’s a Samurai Killer Sudoku Pro made out of 13 grids; and then further still the cages are toroidal, both around the edge of the grid and across the gaps. In other words, the Killer Sudoku Pro regions aren’t bounded by the actual physical layout of the 13-grids – they either jump the gap (in a straight line) or wrap around the edges of the puzzle (again in a straight line, albeit one that jumps to the other side!).
If you like huge puzzles then you should really enjoy this, assuming you can print it out large enough to actually have a chance of solving it! For everyone else, I’ll post some more smaller puzzles soon! It’s not actually very difficult, logically, but completing the whole thing would still take a fair while – perhaps a couple of hours, I think.
The rules are:
- Place 1-9 into each row, column and 3×3 bold-lined box of each of the 13 underlying 9×9 Sudoku grids
- Place numbers into each dashed-line cage so that all together they give the total at the top-left of the cage once the given operation is applied – for subtraction and division start with the largest number in the cage and then subtract/divide-by the other numbers.
- Numbers can not be repeated in a cage.
- Some cages continue across the gaps – just use an imaginary straight-line rule to follow them on and find the rest of the cage (so for example if a cage runs across a gap in the 3rd row down, it continues on the other side of the gap also on the 3rd row down)
- Some cages continue across the edges of the grid – these wrap around to the same row or column on the opposite side of the puzzle
If you try it: Good Luck!
Toroidal Killer Sudoku Pro
May 7th

Toroidal Killer Sudoku Pro puzzle
Here’s something that I’ve actually never seen before – Killer Sudoku with toroidal cages. Perhaps there’s a good reason for that, but it’s time to find out. ![]() This is actually a Killer Sudoku Pro, so it doesn’t just involve addition – but you cannot repeat a number in a cage, unlike in CalcuDoku.
This is actually a Killer Sudoku Pro, so it doesn’t just involve addition – but you cannot repeat a number in a cage, unlike in CalcuDoku.
So the rules are:
- Place 1 to 9 into each row, column and bold-lined 3×3 box
- Place numbers in each cage to add/multiply/subtract/divide up to the total at the top-left of each cage
- Numbers may not repeat in a cage
- Some cages wrap around the edges of the puzzles, continuing directly opposite
This is rated ‘gentle’, and none of the toroidal cages are very large so shouldn’t be too confusing to follow (I hope!).
Good luck!
Consecutive Samurai CalcuDoku
May 5th

Consecutive Samurai CalcuDoku puzzle
Now this is an interesting puzzle! At first glance it looks like it can’t possibly have a unique solution, since there are no givens and only 9 cages on the entire 3-grid Samurai puzzle (made up of 6×6 grids). But in fact it uses only simple logic to solve, and it unravels pretty quickly once you get going. It’s a pretty powerful demonstration of how much you can strip a puzzle back and still keep it entirely reasonable in terms of difficulty. In fact it’s arguably too easy…
The rules are what you’d expect if you’ve been following previous puzzles, but in summary you must: (deep breath!)
- Place 1 to 6 into each row and column of the three underlying 6×6 grids
- Place numbers into each of the bold-lined cages so that they add up to the number at the top-left (or in the case of the 40x cage, multiply up to that value)
- Wherever a white bar divides two squares, the numbers in those two squares must be consecutive (so they must be one of these pairs: 1&2, 2&3, 3&4, 4&5 or 5&6)
- Where no white bar divides two squares, the numbers are non-consecutive
Good luck!


Recent Comments